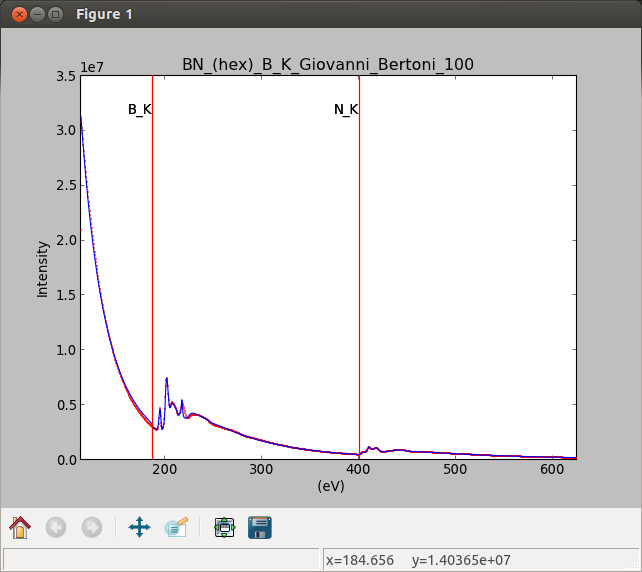
Model fitting¶
HyperSpy can perform curve fitting of one-dimensional signals (spectra) and two-dimensional signals (images) in n-dimensional data sets. Models can be created as a linear combination of predefined components and multiple optimisation algorithms can be used to fit the model to experimental data. Bounds and weights are supported. The syntax for creating both kinds of model is essentially the same as in this documentation any method referred to in the :py:class`~.model.BaseModel` class is available for both kinds.
New in version 1.0: 2D models. Note that this first implementation lacks many of the features of 1D models e.g. plotting. Those will be added in future releases.
Models can be created and and fit to experimental data in both one and two
dimensions i.e. spectra and images respectively. Most of the syntax is
identical in either case. A one-dimensional model is created when a model
is created for a Signal1D whereas a two-
dimensional model is created for a _signals.signal2D.Signal2D.
At present plotting and gradient fitting methods tools for are not yet
provided for the Model2D class.
New in version 0.7: Binned/unbinned signals
Before creating a model verify that the Signal.binned metadata
attribute of the signal is set to the correct value because the resulting
model depends on this parameter. See Binned and unbinned signals for more details.
Creating a model¶
A Model1D can be created for data in the
Signal1D class using the
create_model() method:
>>> s = hs.signals.Signal1D('SomeDataHere') # or load the data from a file
>>> m = s.create_model() # Creates the 1D-Model and asign it to the variable m
Similarly A Model2D can be created for data in the
Signal2D class using the
create_model() method:
>>> im = hs.signals.Signal2D('SomeDataHere') # Load the data from a file
>>> mod = im.create_model() # Create the 2D-Model and asign it to the variable mod
The syntax for creating both one-dimensional and two-dimensional models is thus identical for the user in practice. When a model is created you may be prompted to provide important information not already included in the datafile, e.g.if s is EELS data, you may be asked for the accelerating voltage, convergence and collection semi-angles etc.
Adding components to the model¶
Changed in version 1.0: hyperspy.api.model.components renamed to hyperspy.api.model.components1D
New in version 1.0: hyperspy.api.model.components2D.
In HyperSpy a model consists of a linear combination of components
and various components are available in one (components1d)and
two-dimensions (components2d) to construct a
model.
The following components are currently available for one-dimensional models:
EELSCLEdgeVolumePlasmonDrudePowerLawOffsetExponentialScalableFixedPatternGaussianGaussianHFLorentzianVoigtPolynomialLogisticBleasdaleErfSEEArctanHeavisideStep
New in version 1.0: The following components are currently available for two-dimensional models:
However, this doesn’t mean that you have to limit yourself to this meagre list of functions. A new function can easily be written or a custom function may be specified as below.
Specifying custom components¶
New in version 0.8.1: Expression component
The easiest way to turn a mathematical expression into a component is using the
Expression component. For example, the
following is all you need to create a`Gaussian` component with more sensible
parameters for spectroscopy than the one that ships with HyperSpy:
>>> g = hs.model.components1D.Expression(
... expression="height * exp(-(x - x0) ** 2 * 4 * log(2)/ fwhm ** 2)",
... name="Gaussian",
... position="x0",
... height=1,
... fwhm=1,
... centre=0,
... module="numpy")
Expression uses Sympy internally to turn the string into
a funtion. By default it “translates” the expression using
numpy, but often it is possible to boost performance by using
numexpr instead.
Expression is only useful for analytical
functions. If you know how to write the function with Python, turning it into
a component is very easy modifying the following template:
from hyperspy.component import Component
class My_Component(Component):
"""
"""
def __init__(self, parameter_1=1, parameter_2=2):
# Define the parameters
Component.__init__(self, ('parameter_1', 'parameter_2'))
# Optionally we can set the initial values
self.parameter_1.value = parameter_1
self.parameter_1.value = parameter_1
# The units (optional)
self.parameter_1.units = 'Tesla'
self.parameter_2.units = 'Kociak'
# Once defined we can give default values to the attribute is we want
# For example we fix the attribure_1 (optional)
self.parameter_1.attribute_1.free = False
# And we set the boundaries (optional)
self.parameter_1.bmin = 0.
self.parameter_1.bmax = None
# Optionally, to boost the optimization speed we can define also define
# the gradients of the function we the syntax:
# self.parameter.grad = function
self.parameter_1.grad = self.grad_parameter_1
self.parameter_2.grad = self.grad_parameter_2
# Define the function as a function of the already defined parameters, x
# being the independent variable value
def function(self, x):
p1 = self.parameter_1.value
p2 = self.parameter_2.value
return p1 + x * p2
# Optionally define the gradients of each parameter
def grad_parameter_1(self, x):
"""
Returns d(function)/d(parameter_1)
"""
return 0
def grad_parameter_2(self, x):
"""
Returns d(function)/d(parameter_2)
"""
return x
If you need help with the task please submit your question to the users mailing list.
Changed in version 0.8.1: printing current model components
To print the current components in a model use components of the
variable. A table with component number, attribute name, component name and
component type will be printed:
>>> m
<Model, title: my signal title>
>>> m.components # an empty model
# | Attribute Name | Component Name | Component Type
---- | ------------------------- | ------------------------- | -------------------------
In fact, components may be created automatically in some cases. For example, if
the Signal1D is recognised as EELS data, a power-law background component will
automatically be placed in the model. To add a component first we have to create
an instance of the component. Once the instance has been created we can add the
component to the model using the append() method, e.g. for a type of
data that can be modelled using gaussians we might proceed as follows:
>>> gaussian = hs.model.components1D.Gaussian() # Create a Gaussian function component
>>> m.append(gaussian) # Add it to the model
>>> m.components # Print the model components
# | Attribute Name | Component Name | Component Type
---- | ------------------------- | ------------------------- | -------------------------
0 | Gaussian | Gaussian | Gaussian
>>> gaussian2 = hs.components.Gaussian() # Create another gaussian components
>>> gaussian3 = hs.components.Gaussian() # Create a third gaussian components
We could use the append method two times to add the two gaussians, but when adding multiple components it is handier to use the extend method that enables adding a list of components at once.
>>> m.extend((gaussian2, gaussian3)) # note the double brackets!
>>> m.components
# | Attribute Name | Component Name | Component Type
---- | ------------------------- | ------------------------- | -------------------------
0 | Gaussian | Gaussian | Gaussian
1 | Gaussian_0 | Gaussian_0 | Gaussian
2 | Gaussian_1 | Gaussian_1 | Gaussian
We can customise the name of the components.
>>> gaussian.name = 'Carbon'
>>> gaussian2.name = 'Long Hydrogen name'
>>> gaussian3.name = 'Nitrogen'
>>> m.components
# | Attribute Name | Component Name | Component Type
---- | ------------------------- | ------------------------- | -------------------------
0 | Carbon | Carbon | Gaussian
1 | Long_Hydrogen_name | Long Hydrogen name | Gaussian
2 | Nitrogen | Nitrogen | Gaussian
Two components cannot have the same name.
>>> gaussian2.name = 'Carbon'
Traceback (most recent call last):
File "<ipython-input-5-2b5669fae54a>", line 1, in <module>
g2.name = "Carbon"
File "/home/fjd29/Python/hyperspy/hyperspy/component.py", line 466, in name
"the name " + str(value))
ValueError: Another component already has the name Carbon
It is possible to access the components in the model by their name or by the index in the model.
>>> m
# | Attribute Name | Component Name | Component Type
---- | ------------------------- | ------------------------- | -------------------------
0 | Carbon | Carbon | Gaussian
1 | Long_Hydrogen_name | Long Hydrogen name | Gaussian
2 | Nitrogen | Nitrogen | Gaussian
>>> m[0]
<Carbon (Gaussian component)>
>>> m["Long Hydrogen name"]
<Long Hydrogen name (Gaussian component)>
New in version 0.8.1: components attribute
In addition, the components can be accessed in the
components Model attribute. This is specially
useful when working in interactive data analysis with IPython because it
enables tab completion.
>>> m
# | Attribute Name | Component Name | Component Type
---- | ------------------------- | ------------------------- | -------------------------
0 | Carbon | Carbon | Gaussian
1 | Long_Hydrogen_name | Long Hydrogen name | Gaussian
2 | Nitrogen | Nitrogen | Gaussian
>>> m.components.Long_Hydrogen_name
<Long Hydrogen name (Gaussian component)>
It is possible to “switch off” a component by setting its
active to False. When a components is
switched off, to all effects it is as if it was not part of the model. To
switch it on simply set the active attribute
back to True.
New in version 0.7.1: active_is_multidimensional
In multidimensional signals it is possible to store the value of the
active attribute at each navigation index.
To enable this feature for a given component set the
active_is_multidimensional attribute to
True.
>>> s = hs.signals.Signal1D(np.arange(100).reshape(10,10))
>>> m = s.create_model()
>>> g1 = hs.model.components1D.Gaussian()
>>> g2 = hs.model.components1D.Gaussian()
>>> m.extend([g1,g2])
>>> g1.active_is_multidimensional = True
>>> g1._active_array
array([ True, True, True, True, True, True, True, True, True, True], dtype=bool)
>>> g2._active_array is None
True
>>> m.set_component_active_value(False)
>>> g1._active_array
array([False, False, False, False, False, False, False, False, False, False], dtype=bool)
>>> m.set_component_active_value(True, only_current=True)
>>> g1._active_array
array([ True, False, False, False, False, False, False, False, False, False], dtype=bool)
>>> g1.active_is_multidimensional = False
>>> g1._active_array is None
True
Indexing model¶
New in version 1.0: model indexing
Often it is useful to consider only part of the model - for example at
a particular location (i.e. a slice in the navigation space) or energy range
(i.e. a slice in the signal space). This can be done using exactly the same
syntax that we use for signal indexing (Indexing).
red_chisq and dof are automatically
recomputed for the resulting slices.
>>> s = hs.signals.Signal1D(np.arange(100).reshape(10,10))
>>> m = s.create_model()
>>> m.append(hs.model.components1D.Gaussian())
>>> # select first three navigation pixels and last five signal channels
>>> m1 = m.inav[:3].isig[-5:]
>>> m1.signal1D
<Signal1D, title: , dimensions: (3|5)>
Getting and setting parameter values and attributes¶
print_current_values() prints the value of the
parameters of the components in the current coordinates.
parameters contains a list of the parameters
of a component and free_parameters lists only
the free parameters.
The value of a particular parameter can be accessed in the
value.
If a model contains several components with the same parameters, it is possible
to change them all by using set_parameters_value().
Example:
>>> s = hs.signals.Signal1D(np.arange(100).reshape(10,10))
>>> m = s.create_model()
>>> g1 = hs.model.components1D.Gaussian()
>>> g2 = hs.model.components1D.Gaussian()
>>> m.extend([g1,g2])
>>> m.set_parameters_value('A', 20)
>>> g1.A.map['values']
array([ 20., 20., 20., 20., 20., 20., 20., 20., 20., 20.])
>>> g2.A.map['values']
array([ 20., 20., 20., 20., 20., 20., 20., 20., 20., 20.])
>>> m.set_parameters_value('A', 40, only_current=True)
>>> g1.A.map['values']
array([ 40., 20., 20., 20., 20., 20., 20., 20., 20., 20.])
>>> m.set_parameters_value('A',30, component_list=[g2])
>>> g2.A.map['values']
array([ 30., 30., 30., 30., 30., 30., 30., 30., 30., 30.])
>>> g1.A.map['values']
array([ 40., 20., 20., 20., 20., 20., 20., 20., 20., 20.])
To set the the free state of a parameter change the
free attribute. To change the free state of
all parameters in a component to True use
set_parameters_free(), and
set_parameters_not_free() for setting them to
False. Specific parameter-names can also be specified by using
parameter_name_list, shown in the example:
>>> g = hs.model.components1D.Gaussian()
>>> g.free_parameters
set([<Parameter A of Gaussian component>,
<Parameter sigma of Gaussian component>,
<Parameter centre of Gaussian component>])
>>> g.set_parameters_not_free()
set([])
>>> g.set_parameters_free(parameter_name_list=['A','centre'])
set([<Parameter A of Gaussian component>,
<Parameter centre of Gaussian component>])
Similar functions exist for BaseModel:
set_parameters_free() and
set_parameters_not_free(). Which sets the
free states for the parameters in components
in a model. Specific components and parameter-names can also be specified. For
example:
>>> g1 = hs.model.components1D.Gaussian()
>>> g2 = hs.model.components1D.Gaussian()
>>> m.extend([g1,g2])
>>> m.set_parameters_not_free()
>>> g1.free_parameters
set([])
>>> g2.free_parameters
set([])
>>> m.set_parameters_free(parameter_name_list=['A'])
>>> g1.free_parameters
set([<Parameter A of Gaussian component>])
>>> g2.free_parameters
set([<Parameter A of Gaussian component>])
>>> m.set_parameters_free([g1], parameter_name_list=['sigma'])
>>> g1.free_parameters
set([<Parameter A of Gaussian component>,
<Parameter sigma of Gaussian component>])
>>> g2.free_parameters
set([<Parameter A of Gaussian component>])
The value of a parameter can be coupled to the value of another by setting the
twin attribute.
For example:
>>> gaussian.parameters # Print the parameters of the gaussian components
(A, sigma, centre)
>>> gaussian.centre.free = False # Fix the centre
>>> gaussian.free_parameters # Print the free parameters
set([A, sigma])
>>> m.print_current_values() # Print the current value of all the free parameters
Components Parameter Value
Normalized Gaussian
A 1.000000
sigma 1.000000
Normalized Gaussian
centre 0.000000
A 1.000000
sigma 1.000000
Normalized Gaussian
A 1.000000
sigma 1.000000
centre 0.000000
>>> gaussian2.A.twin = gaussian3.A # Couple the A parameter of gaussian2 to the A parameter of gaussian 3
>>> gaussian2.A.value = 10 # Set the gaussian2 centre value to 10
>>> m.print_current_values()
Components Parameter Value
Carbon
sigma 1.000000
A 1.000000
centre 0.000000
Hydrogen
sigma 1.000000
A 10.000000
centre 10.000000
Nitrogen
sigma 1.000000
A 10.000000
centre 0.000000
>>> gaussian3.A.value = 5 # Set the gaussian1 centre value to 5
>>> m.print_current_values()
Components Parameter Value
Carbon
sigma 1.000000
A 1.000000
centre 0.000000
Hydrogen
sigma 1.000000
A 5.000000
centre 10.000000
Nitrogen
sigma 1.000000
A 5.000000
centre 0.000000
By default the coupling function is the identity function. However it is
possible to set a different coupling function by setting the
twin_function and
twin_inverse_function attributes. For
example:
>>> gaussian2.A.twin_function = lambda x: x**2
>>> gaussian2.A.twin_inverse_function = lambda x: np.sqrt(np.abs(x))
>>> gaussian2.A.value = 4
>>> m.print_current_values()
Components Parameter Value
Carbon
sigma 1.000000
A 1.000000
centre 0.000000
Hydrogen
sigma 1.000000
A 4.000000
centre 10.000000
Nitrogen
sigma 1.000000
A 2.000000
centre 0.000000
>>> gaussian3.A.value = 4
>>> m.print_current_values()
Components Parameter Value
Carbon
sigma 1.000000
A 1.000000
centre 0.000000
Hydrogen
sigma 1.000000
A 16.000000
centre 10.000000
Nitrogen
sigma 1.000000
A 4.000000
centre 0.000000
Fitting the model to the data¶
To fit the model to the data at the current coordinates (e.g. to fit one
spectrum at a particular point in a spectrum-image) use
fit().
The following table summarizes the features of the currently available optimizers:
| Optimizer | Bounds | Error estimation | Method |
|---|---|---|---|
| “leastsq” | No | Yes | least squares |
| “mpfit” | Yes | Yes | least squares |
| “odr” | No | Yes | least squares |
| “fmin” | No | No | least squares, maximum likelihood |
The following example shows how to perfom least squares with error estimation.
First we create data consisting of a line line y = a*x + b with a = 1
and b = 100 and we add white noise to it:
>>> s = hs.signals.SpectrumSimulation(
... np.arange(100, 300))
>>> s.add_gaussian_noise(std=100)
To fit it we create a model consisting of a
Polynomial component of order 1 and fit it
to the data.
>>> m = s.create_model()
>>> line = hs.model.components1D.Polynomial(order=1)
>>> m.append(line)
>>> m.fit()
On fitting completion, the optimized value of the parameters and their estimated standard deviation are stored in the following line attributes:
>>> line.coefficients.value
(0.99246156488437653, 103.67507406125888)
>>> line.coefficients.std
(0.11771053738516088, 13.541061301257537)
When the noise is heterocedastic, only if the
metadata.Signal.Noise_properties.variance attribute of the
Signal1D instance is defined can the errors be
estimated accurately. If the variance is not defined, the standard deviation of
the parameters are still computed and stored in the
std attribute by setting variance equal 1.
However, the value won’t be correct unless an accurate value of the variance is
defined in metadata.Signal.Noise_properties.variance. See
Setting the noise properties for more information.
In the following example, we add poissonian noise to the data instead of gaussian noise and proceed to fit as in the previous example.
>>> s = hs.signals.SpectrumSimulation(
... np.arange(300))
>>> s.add_poissonian_noise()
>>> m = s.create_model()
>>> line = hs.model.components1D.Polynomial(order=1)
>>> m.append(line)
>>> m.fit()
>>> line.coefficients.value
(1.0052331707848698, -1.0723588390873573)
>>> line.coefficients.std
(0.0081710549764721901, 1.4117294994070277)
Because the noise is heterocedastic, the least squares optimizer estimation is biased. A more accurate result can be obtained by using weighted least squares instead that, although still biased for poissonian noise, is a good approximation in most cases.
>>> s.estimate_poissonian_noise_variance(expected_value=hs.signals.Signal1D(np.arange(300)))
>>> m.fit()
>>> line.coefficients.value
(1.0004224896604759, -0.46982916592391377)
>>> line.coefficients.std
(0.0055752036447948173, 0.46950832982673557)
We can use poissonian maximum likelihood estimation instead that is an unbiased estimator for poissonian noise.
>>> m.fit(fitter="fmin", method="ml")
>>> line.coefficients.value
(1.0030718094185611, -0.63590210946134107)
Problems of ill-conditioning and divergence can be ameliorated by using bounded
optimization. Currently, only the “mpfit” optimizer supports bounds. In the
following example a gaussian histogram is fitted using a
Gaussian component using mpfit and bounds on
the centre parameter.
>>> s = hs.signals.BaseSignal(np.random.normal(loc=10, scale=0.01,
size=1e5)).get_histogram()
>>> s.metadata.Signal.binned = True
>>> m = s.create_model()
>>> g1 = hs.model.components1D.Gaussian()
>>> m.append(g1)
>>> g1.centre.value = 7
>>> g1.centre.bmin = 7
>>> g1.centre.bmax = 14
>>> g1.centre.bounded = True
>>> m.fit(fitter="mpfit", bounded=True)
>>> m.print_current_values()
Components Parameter Value
Gaussian
sigma 0.00996345
A 99918.7
centre 9.99976
New in version 0.7: chi-squared and reduced chi-squared
The chi-squared, reduced chi-squared and the degrees of freedom are
computed automatically when fitting. They are stored as signals, in the
chisq, red_chisq and
dof attributes of the model respectively. Note that,
unless metadata.Signal.Noise_properties.variance contains an accurate
estimation of the variance of the data, the chi-squared and reduced
chi-squared cannot be computed correctly. This is also true for
homocedastic noise.
Visualizing the model¶
To visualise the result use the plot() method:
>>> m.plot() # Visualise the results
New in version 0.7.
By default only the full model line is displayed in the plot. In addition, it
is possible to display the individual components by calling
enable_plot_components() or directly using
plot():
>>> m.plot(plot_components=True) # Visualise the results
To disable this feature call disable_plot_components().
New in version 0.7.1: suspend_update() and resume_update()
By default the model plot is automatically updated when any parameter value
changes. It is possible to suspend this feature with
suspend_update(). To resume it use
resume_update().
Setting the initial parameters¶
Non-linear regression often requires setting sensible starting parameters. This can be done by plotting the model and adjusting the parameters by hand.
New in version 0.7: In addition, it is possible to fit a given component independently using
the fit_component() method.
New in version 0.8.5: notebook_interaction(),
If running in a Jupyter Notebook, interactive widgets can be used to
conveniently adjust the parameter values by running
notebook_interaction() for Model,
Component and
Parameter.
Warning
notebook_interaction() functions require
ipywidgets, which is an optional dependency of HyperSpy.
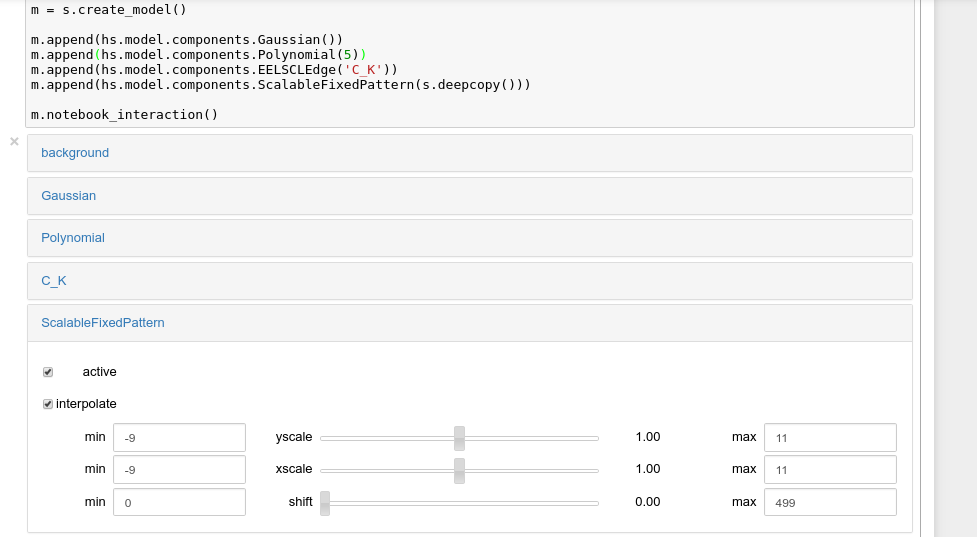
Interactive widgets for the full model in a Jupyter notebook. Drag the sliders to adjust current parameter values. Typing different minimum and maximum values changes the boundaries of the slider.
New in version 0.6: enable_adjust_position() and
disable_adjust_position()
Also, enable_adjust_position() provides an interactive
way of setting the position of the components with a well define position.
disable_adjust_position() disables the tool.
Exclude data from the fitting process¶
The following BaseModel methods can be used to exclude
undesired spectral channels from the fitting process:
set_signal_range()remove_signal_range()reset_signal_range()
Fitting multidimensional datasets¶
To fit the model to all the elements of a multidimensional datataset use
multifit(), e.g.:
>>> m.multifit() # warning: this can be a lengthy process on large datasets
multifit() fits the model at the first position,
store the result of the fit internally and move to the next position until
reaching the end of the dataset.
Sometimes one may like to store and fetch the value of the parameters at a
given position manually. This is possible using
store_current_values() and
fetch_stored_values().
Storing models¶
New in version 1.0: ModelManager
Multiple models can be stored in the same signal. In particular, when
store() is called, a full “frozen” copy of the model is stored
in models. The stored models can be recreated at any time
by calling restore() with the stored model name as an
argument. To remove a model from storage, simply call
remove()
The stored models can be either given a name, or assigned one automatically. The automatic naming follows alphabetical scheme, with the sequence being (a, b, ..., z, aa, ab, ..., az, ba, ...).
Note
If you want to slice a model, you have to perform the operation on the model itself, not its stored version
Warning
Modifying a signal in-place (e.g. map(),
crop(), align1D(),
align2D() and similar) will invalidate all stored models.
This is done intentionally.
Current stored models can be listed by calling models:
>>> m = s.create_model()
>>> m.append(hs.model.components1D.Lorentzian())
>>> m.store('myname')
>>> s.models
└── myname
├── components
│ └── Lorentzian
├── date = 2015-09-07 12:01:50
└── dimensions = (|100)
>>> m.append(hs.model.components1D.Exponential())
>>> m.store() # assign model name automatically
>>> s.models
├── a
│ ├── components
│ │ ├── Exponential
│ │ └── Lorentzian
│ ├── date = 2015-09-07 12:01:57
│ └── dimensions = (|100)
└── myname
├── components
│ └── Lorentzian
├── date = 2015-09-07 12:01:50
└── dimensions = (|100)
>>> m1 = s.models.restore('myname')
>>> m1.components
# | Attribute Name | Component Name | Component Type
---- | ------------------------- | ------------------------- | -------------------------
0 | Lorentzian | Lorentzian | Lorentzian
Saving and loading the result of the fit¶
New in version 1.0.
To save a model, a convenience function save() is provided,
which stores the current model into its signal and saves the signal. As
described in storing_models, more than just one model can be saved with
one signal.
>>> m = s.create_model()
>>> # analysis and fitting goes here
>>> m.save('my_filename', 'model_name')
>>> l = hs.load('my_filename.hdf5')
>>> m = l.models.restore('model_name') # or l.models.model_name.restore()
For older versions of HyperSpy (before 0.9), the instructions were as follows:
Note that this method is known to be brittle i.e. there is no guarantee that a version of HyperSpy different from the one used to save the model will be able to load it successfully. Also, it is advisable not to use this method in combination with functions that alter the value of the parameters interactively (e.g. enable_adjust_position) as the modifications made by this functions are normally not stored in the IPython notebook or Python script.
To save a model:
- Save the parameter arrays to a file using
save_parameters2file().- Save all the commands that used to create the model to a file. This can be done in the form of an IPython notebook or a Python script.
- (Optional) Comment out or delete the fitting commangs (e.g. multifit).
To recreate the model:
- Execute the IPython notebook or Python script.
- Use
load_parameters_from_file()to load back the parameter values and arrays.
Batch setting of parameter attributes¶
New in version 0.6.
The following methods can be used to ease the task of setting some important parameter attributes:
Smart Adaptive Multi-dimensional Fitting (SAMFire)¶
New in version 1.0: SAMFire
SAMFire (Smart Adaptive Multi-dimensional Fitting) is an algorithm created to reduce the starting value (or local / false minima) problem, which often arises when fitting multi-dimensional datasets.
The algorithm will be described in full when accompanying paper is published, but we are making the implementation available now.
The idea¶
The main idea of SAMFire is to change two things compared to the traditional way of fitting datasets with many dimensions in the navigation space:
- Pick a more sensible pixel fitting order.
- Calculate the pixel starting parameters from already fitted parts of the dataset.
Both of these aspects are linked one to another and are represented by two different strategy families that SAMFfire uses while operating.
Strategies¶
During operation SAMFire uses a list of strategies to determine how to select the next pixel and estimate its starting parameters. Only one strategy is used at a time. Next strategy is chosen when no new pixels are can be fitted with the current strategy. Once either the strategy list is exhausted or the full dataset fitted, the algorithm terminates.
There are two families of strategies. In each family there may be many strategies, using different statistical or significance measures.
As a rule of thumb, the first strategy in the list should always be from the local family, followed by a strategy from the global family.
Local strategy family¶
These strategies assume that locally neighbouring pixels are similar. As a result, the pixel fitting order seems to follow data-suggested order, and the starting values are computed from the surrounding already fitted pixels.
More information about the exact procedure will be available once the accompanying paper is published.
Global strategy family¶
Global strategies assume that the navigation coordinates of each pixel bear no relation to it’s signal (i.e. the location of pixels is meaningless). As a result, the pixels are selected at random to ensure uniform sampling of the navigation space.
A number of candidate starting values are computed form global statistical measures. These values are all attempted in order until a satisfactory result is found (not necessarily testing all available starting guesses). As a result, on average each pixel requires significantly more computations when compared to a local strategy.
More information about the exact procedure will be available once the accompanying paper is published.
Seed points¶
Due to the strategies using already fitted pixels to estimate the starting values, at least one pixel has to be fitted beforehand by the user.
The seed pixel(s) should be selected to require the most complex model present in the dataset, however in-built goodness of fit checks ensure that only sufficiently well fitted values are allowed to propagate.
If the dataset consists of regions (in the navigation space) of highly dissimilar pixels, often called “domain structures”, at least one seed pixel should be given for each unique region.
If the starting pixels were not optimal, only part of the dataset will be fitted. In such cases it is best to allow the algorithm terminate, then provide new (better) seed pixels by hand, and restart SAMFire. It will use the new seed together with the already computed parts of the data.
Usage¶
After creating a model and fitting suitable seed pixels, to fit the rest of the multi-dimensional dataset using SAMFire we must craete a SAMFire instance as follows:
>>> samf = m.create_samfire(workers=None, ipyparallel=False)
By default SAMFire will look for an ipyparallel cluster for the
workers for around 30 seconds. If none is available, it will use
multiprocessing instead. However, if you are not planning to use ipyparallel,
it’s recommended specify it explicitly via the ipyparallel=False argument,
to use the fall-back option of multiprocessing.
By default a new SAMFire object already has two (and currently only) strategies added to its strategist list:
>>> samf.strategies
A | # | Strategy
-- | ---- | -------------------------
x | 0 | Reduced chi squared strategy
| 1 | Histogram global strategy
The currently active strategy is marked by an ‘x’ in the first column.
If a new datapoint (i.e. pixel) is added manually, the “database” of the
currently active strategy has to be refreshed using the
refresh_database() call.
The current strategy “database” can be plotted using the
plot() method.
Whilst SAMFire is running, each pixel is checked by a goodness_test,
which is by default red_chisq_test, checking the
reduced chi-squared to be in the bounds of [0, 2].
This tolerance can (and most likely should!) be changed appropriately for the data as follows:
>>> samf.metadata.goodness_test.tolerance = 0.3 # use a sensible value
The SAMFire managed multi-dimensional fit can be started using the
start() method. All keyword arguments are passed to
the underlying (i.e. usual) fit() call:
>>> samf.start(fitter='mpfit', bounded=True)