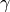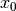hyperspy._components package

Submodules

hyperspy._components.arctan module

class hyperspy._components.arctan.Arctan(A=1.0, k=1.0, x0=1.0, minimum_at_zero=False)

Bases: hyperspy.component.Component

Arctan function component

f(x) = A*arctan{k*(x-x0)}

Parameter Attribute
   
A A
k k
x x
x0 x0
function(x)
grad_A(x)
grad_k(x)
grad_x0(x)

hyperspy._components.bleasdale module

class hyperspy._components.bleasdale.Bleasdale

Bases: hyperspy.component.Component

Bleasdale function component.

f(x) = (a+b*x)^(-1/c)

a

Float

b

Float

c

Float

function(x)
grad_a(x)

Returns d(function)/d(parameter_1)

grad_b(x)

Returns d(function)/d(parameter_1)

grad_c(x)

Returns d(function)/d(parameter_1)

hyperspy._components.eels_cl_edge module

class hyperspy._components.eels_cl_edge.EELSCLEdge(element_subshell, GOS=None)

Bases: hyperspy.component.Component

EELS core loss ionisation edge from hydrogenic or tabulated Hartree-Slater GOS with splines for fine structure fitting.

Hydrogenic GOS are limited to K and L shells.

Currently it only supports Peter Rez’s Hartree Slater cross sections parametrised as distributed by Gatan in their Digital Micrograph (DM) software. If Digital Micrograph is installed in the system HyperSpy in the standard location HyperSpy should find the path to the HS GOS folder. Otherwise, the location of the folder can be defined in HyperSpy preferences, which can be done through hs.preferences.gui() or the hs.preferences.EELS.eels_gos_files_path variable.

Parameters:
  • element_subshell ({str, dict}) – Usually a string, for example, ‘Ti_L3’ for the GOS of the titanium L3 subshell. If a dictionary is passed, it is assumed that Hartree Slater GOS was exported using GOS.as_dictionary, and will be reconstructed.
  • GOS ({'hydrogenic', 'Hartree-Slater', None}) – The GOS to use. If None it will use the Hartree-Slater GOS if they are available, otherwise it will use the hydrogenic GOS.
onset_energy

Parameter – The edge onset position

intensity

Parameter – The factor by which the cross section is multiplied, what in favourable cases is proportional to the number of atoms of the element. It is a component.Parameter instance. It is fixed by default.

fine_structure_coeff

Parameter – The coefficients of the spline that fits the fine structure. Fix this parameter to fix the fine structure. It is a component.Parameter instance.

effective_angle

Parameter – The effective collection semi-angle. It is automatically calculated by set_microscope_parameters. It is a component.Parameter instance. It is fixed by default.

fine_structure_smoothing

float between 0 and 1 – Controls the level of smoothing of the fine structure model. Decreasing the value increases the level of smoothing.

fine_structure_active

bool – Activates/deactivates the fine structure feature.

E0
collection_angle
convergence_angle
fine_structure_active
fine_structure_coeff_to_txt(filename)
fine_structure_smoothing

Controls the level of the smoothing of the fine structure.

It must a real number between 0 and 1. The higher close to 0 the higher the smoothing.

fine_structure_width
function(E)

Returns the number of counts in barns

get_fine_structure_as_signal1D()

Returns a spectrum containing the fine structure.

Notes

The fine structure is corrected from multiple scattering if the model was convolved with a low-loss spectrum

grad_intensity(E)
gui(display=True, toolkit=None, **kwargs)

Display or return interactive GUI element if available.

Parameters:
  • display (bool) – If True, display the user interface widgets. If False, return the widgets container in a dictionary, usually for customisation or testing.
  • toolkit (str, iterable of strings or None) – If None (default), all available widgets are displayed or returned. If string, only the widgets of the selected toolkit are displayed if available. If an interable of toolkit strings, the widgets of all listed toolkits are displayed or returned.
set_microscope_parameters(E0, alpha, beta, energy_scale)
Parameters:
  • E0 (float) – Electron beam energy in keV.
  • alpha (float) – Convergence semi-angle in mrad.
  • beta (float) – Collection semi-angle in mrad.
  • energy_scale (float) – The energy step in eV.
txt_to_fine_structure_coeff(filename)

hyperspy._components.eels_double_power_law module

class hyperspy._components.eels_double_power_law.DoublePowerLaw(A=1e-05, r=3.0, origin=0.0)

Bases: hyperspy.component.Component

function(x)

Given an one dimensional array x containing the energies at which you want to evaluate the background model, returns the background model for the current parameters.

grad_A(x)
grad_origin(x)
grad_r(x)
grad_ratio(x)
grad_shift(x)

hyperspy._components.eels_vignetting module

class hyperspy._components.eels_vignetting.Vignetting

Bases: hyperspy.component.Component

Model the vignetting of the lens with a cos^4 law multiplied by lines on the edges

fix_cos_vignetting()
fix_side_vignetting()
free_cos_vignetting()
free_side_vignetting()
function(x)

hyperspy._components.error_function module

class hyperspy._components.error_function.Erf

Bases: hyperspy.component.Component

Error function component

A

float

sigma

float

origin

float

function(x)
grad_A(x)
grad_origin(x)
grad_sigma(x)

hyperspy._components.exponential module

class hyperspy._components.exponential.Exponential

Bases: hyperspy.component.Component

Exponentian function components

f(x) = A*e^{-x/k}

Parameter Attribute
   
A A
k tau
function(x)
grad_A(x)
grad_tau(x)

hyperspy._components.expression module

class hyperspy._components.expression.Expression(expression, name, position=None, module='numpy', autodoc=True, add_rotation=False, rotation_center=None, **kwargs)

Bases: hyperspy.component.Component

Create a component from a string expression.

compile_function(module='numpy', position=False)

hyperspy._components.gaussian module

class hyperspy._components.gaussian.Gaussian(A=1.0, sigma=1.0, centre=0.0)

Bases: hyperspy.component.Component

Normalized gaussian function component

f(x) = \frac{a}{\sqrt{2\pi c^{2}}}exp\left[-\frac{\left(x-b\right)^{2}}{2c^{2}}\right]

Parameter Attribute
   
a A
b centre
c sigma

For convenience the fwhm attribute can be used to get and set the full-with-half-maximum.

See also

hyperspy._components.gaussianhf.GaussianHF

estimate_parameters(signal, x1, x2, only_current=False)

Estimate the gaussian by calculating the momenta.

Parameters:
  • signal (Signal1D instance) –
  • x1 (float) – Defines the left limit of the spectral range to use for the estimation.
  • x2 (float) – Defines the right limit of the spectral range to use for the estimation.
  • only_current (bool) – If False estimates the parameters for the full dataset.
Returns:
Return type:

bool

Notes

Adapted from http://www.scipy.org/Cookbook/FittingData

Examples

>>> g = hs.model.components1D.Gaussian()
>>> x = np.arange(-10, 10, 0.01)
>>> data = np.zeros((32, 32, 2000))
>>> data[:] = g.function(x).reshape((1, 1, 2000))
>>> s = hs.signals.Signal1D(data)
>>> s.axes_manager._axes[-1].offset = -10
>>> s.axes_manager._axes[-1].scale = 0.01
>>> g.estimate_parameters(s, -10, 10, False)
function(x)
fwhm
grad_A(x)
grad_centre(x)
grad_sigma(x)

hyperspy._components.gaussian2d module

class hyperspy._components.gaussian2d.Gaussian2D(A=1.0, sigma_x=1.0, sigma_y=1.0, centre_x=0.0, centre_y=0.0)

Bases: hyperspy.component.Component

Normalized 2D elliptical gaussian function component

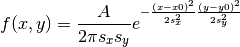
f(x,y) = \frac{A}{2\pi s_x s_y}e^{-\frac{\left(x-x0\right) ^{2}}{2s_{x}^{2}}\frac{\left(y-y0\right)^{2}}{2s_{y}^{2}}}

Parameter Attribute
   
a amplitude
x0,y0 centre
s_x,s_y sigma
function(x, y)
fwhm_x
fwhm_y

hyperspy._components.gaussianhf module

class hyperspy._components.gaussianhf.GaussianHF(height=1.0, fwhm=1.0, centre=0.0, **kwargs)

Bases: hyperspy._components.expression.Expression

Normalized gaussian function component, with a fwhm parameter instead of the sigma parameter, and a height parameter instead of the A parameter (scaling difference of sigma * sqrt(2*Pi)). This makes the parameter vs. peak maximum independent of sigma, and thereby makes locking of the parameter more viable. As long as there is no binning, the height parameter corresponds directly to the peak maximum, if not, the value is scaled by a linear constant (signal_axis.scale).

f(x) = h \sqrt{2\pi}\mathrm{exp}{\left[-\frac{4 \log{2}\left(x-c\right)^{2}}{W^{2}}\right]}

Parameters:
  • height (float) – The height of the peak. If there is no binning, this corresponds directly to the maximum, otherwise the maximum divided by signal_axis.scale
  • centre (float) – Location of the gaussian maximum, also the mean position.
  • fwhm (float) – The full width half maximum value, i.e. the width of the gaussian at half the value of gaussian peak (at centre).
  • **kwargs – Extra keyword arguments are passes to the Expression component. An useful keyword argument that can be used to speed up the component is module. See the Expression component documentation for details.

The helper properties sigma and A are also defined for compatibility with Gaussian component.

See also

hyperspy.components.Gaussian

A
estimate_parameters(signal, x1, x2, only_current=False)

Estimate the gaussian by calculating the momenta.

Parameters:
  • signal (Signal1D instance) –
  • x1 (float) – Defines the left limit of the spectral range to use for the estimation.
  • x2 (float) – Defines the right limit of the spectral range to use for the estimation.
  • only_current (bool) – If False estimates the parameters for the full dataset.
Returns:
Return type:

bool

Notes

Adapted from http://www.scipy.org/Cookbook/FittingData

Examples

>>> g = hs.model.components1D.GaussianHF()
>>> x = np.arange(-10, 10, 0.01)
>>> data = np.zeros((32, 32, 2000))
>>> data[:] = g.function(x).reshape((1, 1, 2000))
>>> s = hs.signals.Signal1D(data)
>>> s.axes_manager._axes[-1].offset = -10
>>> s.axes_manager._axes[-1].scale = 0.01
>>> g.estimate_parameters(s, -10, 10, False)
integral_as_signal()

Utility function to get gaussian integral as Signal1D

sigma

hyperspy._components.heaviside module

class hyperspy._components.heaviside.HeavisideStep(A=1, n=0)

Bases: hyperspy.component.Component

The Heaviside step function

System Message: WARNING/2 (f(x) = \begin{cases} 0 $ \quad \text{if } x < n \\ A/2 $ \quad \text{if } x = n \\ A $ \quad \text{if } x > n \\ \end{cases})

latex exited with error [stdout] This is pdfTeX, Version 3.14159265-2.6-1.40.19 (TeX Live 2019/dev/Debian) (preloaded format=latex) restricted \write18 enabled. entering extended mode (./math.tex LaTeX2e <2018-04-01> patch level 5 (/usr/share/texlive/texmf-dist/tex/latex/base/article.cls Document Class: article 2014/09/29 v1.4h Standard LaTeX document class (/usr/share/texlive/texmf-dist/tex/latex/base/size12.clo)) (/usr/share/texlive/texmf-dist/tex/latex/base/inputenc.sty (/usr/share/texlive/texmf-dist/tex/latex/ucs/utf8x.def)) (/usr/share/texlive/texmf-dist/tex/latex/ucs/ucs.sty (/usr/share/texlive/texmf-dist/tex/latex/ucs/data/uni-global.def)) (/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsmath.sty For additional information on amsmath, use the `?' option. (/usr/share/texlive/texmf-dist/tex/latex/amsmath/amstext.sty (/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsgen.sty)) (/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsbsy.sty) (/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsopn.sty)) (/usr/share/texlive/texmf-dist/tex/latex/amscls/amsthm.sty) (/usr/share/texlive/texmf-dist/tex/latex/amsfonts/amssymb.sty (/usr/share/texlive/texmf-dist/tex/latex/amsfonts/amsfonts.sty)) (/usr/share/texlive/texmf-dist/tex/latex/anyfontsize/anyfontsize.sty) (/usr/share/texlive/texmf-dist/tex/latex/tools/bm.sty) No file math.aux. (/usr/share/texlive/texmf-dist/tex/latex/ucs/ucsencs.def) (/usr/share/texlive/texmf-dist/tex/latex/amsfonts/umsa.fd) (/usr/share/texlive/texmf-dist/tex/latex/amsfonts/umsb.fd) ! Missing $ inserted. <inserted text> $ l.19 \end{cases}\end{split} ! Missing $ inserted. <inserted text> $ l.19 \end{cases}\end{split} ! Missing $ inserted. <inserted text> $ l.19 \end{cases}\end{split} ! Missing $ inserted. <inserted text> $ l.19 \end{cases}\end{split} ! Missing $ inserted. <inserted text> $ l.19 \end{cases}\end{split} ! Missing $ inserted. <inserted text> $ l.19 \end{cases}\end{split} [1] (./math.aux) ) (see the transcript file for additional information) Output written on math.dvi (1 page, 480 bytes). Transcript written on math.log.
function(x)
grad_A(x)
grad_n(x)

hyperspy._components.logistic module

class hyperspy._components.logistic.Logistic

Bases: hyperspy.component.Component

Logistic function component

f(x) = a/(1+b*exp(-c*(x-origin)))

a

Float

b

Float

c

Float

origin

Float

function(x)
grad_a(x)

Returns d(function)/d(parameter_1)

grad_b(x)

Returns d(function)/d(parameter_1)

grad_c(x)

Returns d(function)/d(parameter_1)

grad_origin(x)

Returns d(function)/d(parameter_1)

hyperspy._components.lorentzian module

class hyperspy._components.lorentzian.Lorentzian(A=1.0, gamma=1.0, centre=0.0)

Bases: hyperspy.component.Component

Cauchy-Lorentz distribution (a.k.a. Lorentzian function) component

f(x)=\frac{a}{\pi}\left[\frac{\gamma}{\left(x-x_{0}\right)^{2}+\gamma^{2}}\right]

Parameter Attribute
   
a A
\gamma gamma
x_0 centre
function(x)
grad_A(x)
grad_centre(x)
grad_gamma(x)

hyperspy._components.offset module

class hyperspy._components.offset.Offset(offset=0.0)

Bases: hyperspy.component.Component

Component to add a constant value in the y-axis

f(x) = k + x

Parameter Attribute
   
k offset
estimate_parameters(signal, x1, x2, only_current=False)

Estimate the parameters by the two area method

Parameters:
  • signal (BaseSignal instance) –
  • x1 (float) – Defines the left limit of the spectral range to use for the estimation.
  • x2 (float) – Defines the right limit of the spectral range to use for the estimation.
  • only_current (bool) – If False estimates the parameters for the full dataset.
Returns:
Return type:

bool
function(x)
static grad_offset(x)

hyperspy._components.pes_core_line_shape module

class hyperspy._components.pes_core_line_shape.PESCoreLineShape(A=1.0, FWHM=1.0, origin=0.0)

Bases: hyperspy.component.Component

function(x)

Given an one dimensional array x containing the energies at which you want to evaluate the background model, returns the background model for the current parameters.

grad_A(x)
grad_FWHM(x)
grad_ab(x)
grad_origin(x)

hyperspy._components.pes_see module

class hyperspy._components.pes_see.SEE(A=1.0, Phi=1.0, B=0.0, sigma=0)

Bases: hyperspy.component.Component

Secondary electron emission component for Photoemission Spectroscopy

A

float

Phi

float

B

float

sigma

float – Resolution parameter.

function(x)
grad_A(x)
grad_B(x)
grad_Phi(x)
grad_sigma(x)

hyperspy._components.polynomial module

class hyperspy._components.polynomial.Polynomial(order=2)

Bases: hyperspy.component.Component

n-order polynomial component.

Polynomial component defined by the coefficients parameters which is an array of len the order of the polynomial.

For example, the [1,2,3] coefficients define the following 3rd order polynomial: f(x) = 1x² + 2x + 3

coeffcients

array

estimate_parameters(signal, x1, x2, only_current=False)

Estimate the parameters by the two area method

Parameters:
  • signal (Signal1D instance) –
  • x1 (float) – Defines the left limit of the spectral range to use for the estimation.
  • x2 (float) – Defines the right limit of the spectral range to use for the estimation.
  • only_current (bool) – If False estimates the parameters for the full dataset.
Returns:
Return type:

bool
function(x)
get_polynomial_order()
grad_coefficients(x)
grad_one_coefficient(x, index)

Returns the gradient of one coefficient

hyperspy._components.power_law module

class hyperspy._components.power_law.PowerLaw(A=1000000.0, r=3.0, origin=0.0)

Bases: hyperspy.component.Component

Power law component

f(x) = A*(x-x0)^-r

Parameter Attribute
   
A A
r r
x0 origin

The left_cutoff parameter can be used to set a lower threshold from which the component will return 0.

estimate_parameters(signal, x1, x2, only_current=False, out=False)

Estimate the parameters by the two area method

Parameters:
  • signal (Signal1D instance) –
  • x1 (float) – Defines the left limit of the spectral range to use for the estimation.
  • x2 (float) – Defines the right limit of the spectral range to use for the estimation.
  • only_current (bool) – If False, estimates the parameters for the full dataset.
  • out (bool) – If True, returns the result arrays directly without storing in the parameter maps/values. The returned order is (A, r).
Returns:
Return type:

{bool, tuple of values}
function(x)
grad_A(x)
grad_origin(x)
grad_r(x)

hyperspy._components.rc module

class hyperspy._components.rc.RC(V=1, V0=0, tau=1.0)

Bases: hyperspy.component.Component

function(x)

hyperspy._components.scalable_fixed_pattern module

class hyperspy._components.scalable_fixed_pattern.ScalableFixedPattern(signal1D, yscale=1.0, xscale=1.0, shift=0.0, interpolate=True)

Bases: hyperspy.component.Component

Fixed pattern component with interpolation support.

f(x) = a*s(b*x-x0) + c
Parameter Attribute
   
a yscale
b xscale
x0 shift

The fixed pattern is defined by a single spectrum which must be provided to the ScalableFixedPattern constructor, e.g.:

In [1]: s = load('my_spectrum.hspy')
In [2]: my_fixed_pattern = components.ScalableFixedPattern(s))
yscale, xscale, shift

Float

interpolate

Bool – If False no interpolation is performed and only a y-scaled spectrum is returned.

prepare_interpolator : method to fine tune the interpolation
function(x)
grad_yscale(x)
gui(display=True, toolkit=None, **kwargs)

Display or return interactive GUI element if available.

Parameters:
  • display (bool) – If True, display the user interface widgets. If False, return the widgets container in a dictionary, usually for customisation or testing.
  • toolkit (str, iterable of strings or None) – If None (default), all available widgets are displayed or returned. If string, only the widgets of the selected toolkit are displayed if available. If an interable of toolkit strings, the widgets of all listed toolkits are displayed or returned.
prepare_interpolator(kind='linear', fill_value=0, **kwargs)

Prepare interpolation.

Parameters:
  • x (array) – The spectral axis of the fixed pattern
  • kind (str or int, optional) – Specifies the kind of interpolation as a string (‘linear’, ‘nearest’, ‘zero’, ‘slinear’, ‘quadratic, ‘cubic’) or as an integer specifying the order of the spline interpolator to use. Default is ‘linear’.
  • fill_value (float, optional) – If provided, then this value will be used to fill in for requested points outside of the data range. If not provided, then the default is NaN.

Notes

Any extra keyword argument is passed to scipy.interpolate.interp1d

hyperspy._components.voigt module

class hyperspy._components.voigt.Voigt

Bases: hyperspy.component.Component

Voigt profile component with support for shirley background, non_isochromaticity,transmission_function corrections and spin orbit splitting specially suited for Photoemission spectroscopy data analysis.

f(x) = G(x)*L(x) where G(x) is the Gaussian function and L(x) is the Lorentzian function

area

Parameter

centre

Parameter

FWHM

Parameter

gamma

Parameter

resolution

Parameter

shirley_background

Parameter

non_isochromaticity

Parameter

transmission_function

Parameter

spin_orbit_splitting

Bool

spin_orbit_branching_ratio

float

spin_orbit_splitting_energy

float

estimate_parameters(signal, E1, E2, only_current=False)

Estimate the voigt function by calculating the momenta the gaussian.

Parameters:
  • signal (Signal1D instance) –
  • x1 (float) – Defines the left limit of the spectral range to use for the estimation.
  • x2 (float) – Defines the right limit of the spectral range to use for the estimation.
  • only_current (bool) – If False estimates the parameters for the full dataset.
Returns:
Return type:

bool

Notes

Adapted from http://www.scipy.org/Cookbook/FittingData

Examples

>>> g = hs.model.components1D.Gaussian()
>>> x = np.arange(-10,10, 0.01)
>>> data = np.zeros((32,32,2000))
>>> data[:] = g.function(x).reshape((1,1,2000))
>>> s = hs.signals.Signal1D({'data' : data})
>>> s.axes_manager.axes[-1].offset = -10
>>> s.axes_manager.axes[-1].scale = 0.01
>>> g.estimate_parameters(s, -10,10, False)
function(x)
hyperspy._components.voigt.voigt(x, FWHM=1, gamma=1, center=0, scale=1)

Voigt lineshape.

The voigt peak is the convolution of a Lorentz peak with a Gaussian peak.

The formula used to calculate this is:

z(x) = (x + 1j gamma) / (sqrt(2) sigma)
w(z) = exp(-z**2) erfc(-1j z) / (sqrt(2 pi) sigma)

V(x) = scale Re(w(z(x-center)))
Parameters:
  • gamma (real) – The half-width half-maximum of the Lorentzian
  • FWHM (real) – The FWHM of the Gaussian
  • center (real) – Location of the center of the peak
  • scale (real) – Value at the highest point of the peak

Notes

Ref: W.I.F. David, J. Appl. Cryst. (1986). 19, 63-64

adjusted to use stddev and HWHM rather than FWHM parameters

hyperspy._components.volume_plasmon_drude module

class hyperspy._components.volume_plasmon_drude.VolumePlasmonDrude(intensity=1.0, plasmon_energy=15.0, fwhm=1.5)

Bases: hyperspy.component.Component

Drude volume plasmon energy loss function component, the energy loss function is defined as:

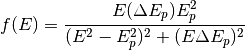
f(E) = \frac{E(\Delta E_p)E_p^2}{(E^2-E_p^2)^2+(E\Delta E_p)^2}

Parameter Attribute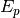
E_p plasmon_energy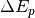
\Delta E_p fwhm
intensity intensity

Notes

Refer to Egerton, R. F., Electron Energy-Loss Spectroscopy in the Electron Microscope, 2nd edition, Plenum Press 1996, pp. 154-158 for details, including original equations.

function(x)
grad_fwhm(x)
grad_intensity(x)
grad_plasmon_energy(x)

Module contents