hyperspy._signals.dielectric_function module¶

class hyperspy._signals.dielectric_function.DielectricFunction_mixin¶

Bases: object

get_number_of_effective_electrons(nat, cumulative=False)¶

Compute the number of effective electrons using the Bethe f-sum rule.

The Bethe f-sum rule gives rise to two definitions of the effective number (see [Egerton2011]), neff1 and neff2:

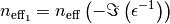
$n_{\mathrm{eff_{1}}} = n_{\mathrm{eff}}\left(-\Im\left(\epsilon^{-1}\right)\right)$

and:

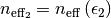
$n_{\mathrm{eff_{2}}} = n_{\mathrm{eff}}\left(\epsilon_{2}\right)$

This method computes and return both.

Parameters:	nat (float) – Number of atoms (or molecules) per unit volume of the sample. cumulative (bool) – If False calculate the number of effective electrons up to the higher energy-loss of the spectrum. If True, calculate the number of effective electrons as a function of the energy-loss up to the higher energy-loss of the spectrum. True is only supported by SciPy newer than 0.13.2.
Returns:	neff1, neff2 – Signal1D instances containing neff1 and neff2. The signal and navigation dimensions are the same as the current signal if cumulative is True, otherwise the signal dimension is 0 and the navigation dimension is the same as the current signal.
Return type:	Signal1D

Notes

Ray Egerton, “Electron Energy-Loss

Spectroscopy in the Electron Microscope”, Springer-Verlag, 2011.