hyperspy.external.astroML.histtools module¶

Tools for working with distributions

class hyperspy.external.astroML.histtools.KnuthF(data)¶

Bases: object

Class which implements the function minimized by knuth_bin_width

Parameters:	data (array-like, one dimension) – data to be histogrammed

Notes

the function F is given by

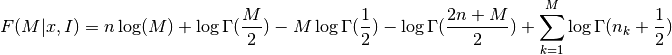
$F(M|x,I) = n\log(M) + \log\Gamma(\frac{M}{2}) - M\log\Gamma(\frac{1}{2}) - \log\Gamma(\frac{2n+M}{2}) + \sum_{k=1}^M \log\Gamma(n_k + \frac{1}{2})$

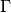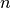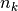where $\Gamma$ is the Gamma function, $n$ is the number of data points, $n_k$ is the number of measurements in bin $k$ .

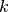See also

knuth_bin_width, astroML.plotting.hist

bins(M)¶: Return the bin edges given a width dx

eval(M)¶

Evaluate the Knuth function

Parameters:	dx (float) – Width of bins
Returns:	F – evaluation of the negative Knuth likelihood function: smaller values indicate a better fit.
Return type:	float

hyperspy.external.astroML.histtools.dasky_freedman_bin_width(data, return_bins=True)¶

Dask version of freedman_bin_width

Parameters:

data (dask array) – the data
return_bins (bool (optional)) – if True, then return the bin edges

Returns:

width (float) – optimal bin width using Scott’s rule
bins (ndarray) – bin edges: returned if return_bins is True

Notes

The optimal bin width is

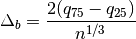
$\Delta_b = \frac{2(q_{75} - q_{25})}{n^{1/3}}$

where 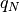$q_{N}$ is the 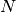$N$ percent quartile of the data, and 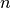$n$ is the number of data points.

See also

knuth_bin_width(), scotts_bin_width(), astroML.plotting.hist()

hyperspy.external.astroML.histtools.dasky_histogram(a, bins=10, **kwargs)¶

Enhanced histogram for dask arrays. The range keyword is ignored. Reads the data at most two times - once to determine best bins (if required), and second time to actually calculate the histogram.

Parameters:

a (array_like) – array of data to be histogrammed
bins (int or list or str (optional)) – If bins is a string, then it must be one of: ‘scotts’ : use Scott’s rule to determine bins ‘freedman’ : use the Freedman-Diaconis rule to determine bins
keyword arguments are described in numpy.hist() (other) –

Returns:

hist (array) – The values of the histogram. See normed and weights for a description of the possible semantics.
bin_edges (array of dtype float) – Return the bin edges (length(hist)+1).

See also

numpy.histogram(), astroML.plotting.hist()

hyperspy.external.astroML.histtools.dasky_scotts_bin_width(data, return_bins=True)¶

Dask version of scotts_bin_width

Parameters:

data (dask array) – the data
return_bins (bool (optional)) – if True, then return the bin edges

Returns:

width (float) – optimal bin width using Scott’s rule
bins (ndarray) – bin edges: returned if return_bins is True

Notes

The optimal bin width is:

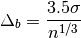
$\Delta_b = \frac{3.5\sigma}{n^{1/3}}$

where 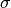$\sigma$ is the standard deviation of the data, and 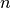$n$ is the number of data points.

See also

knuth_bin_width(), freedman_bin_width(), astroML.plotting.hist()

hyperspy.external.astroML.histtools.freedman_bin_width(data, return_bins=False)¶

Return the optimal histogram bin width using the Freedman-Diaconis rule

Parameters:

data (array-like, ndim=1) – observed (one-dimensional) data
return_bins (bool (optional)) – if True, then return the bin edges

Returns:

width (float) – optimal bin width using Scott’s rule
bins (ndarray) – bin edges: returned if return_bins is True

Notes

The optimal bin width is

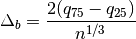
$\Delta_b = \frac{2(q_{75} - q_{25})}{n^{1/3}}$

where 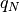$q_{N}$ is the 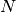$N$ percent quartile of the data, and 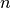$n$ is the number of data points.

See also

knuth_bin_width(), scotts_bin_width(), astroML.plotting.hist()

hyperspy.external.astroML.histtools.histogram(a, bins=10, range=None, **kwargs)¶

Enhanced histogram

This is a histogram function that enables the use of more sophisticated algorithms for determining bins. Aside from the bins argument allowing a string specified how bins are computed, the parameters are the same as numpy.histogram().

Parameters:

a (array_like) – array of data to be histogrammed
bins (int or list or str (optional)) – If bins is a string, then it must be one of: ‘blocks’ : use bayesian blocks for dynamic bin widths ‘knuth’ : use Knuth’s rule to determine bins ‘scotts’ : use Scott’s rule to determine bins ‘freedman’ : use the Freedman-diaconis rule to determine bins
range (tuple or None (optional)) – the minimum and maximum range for the histogram. If not specified, it will be (x.min(), x.max())
keyword arguments are described in numpy.hist() (other) –

Returns:

hist (array) – The values of the histogram. See normed and weights for a description of the possible semantics.
bin_edges (array of dtype float) – Return the bin edges (length(hist)+1).

See also

numpy.histogram(), astroML.plotting.hist()

hyperspy.external.astroML.histtools.knuth_bin_width(data, return_bins=False)¶

Return the optimal histogram bin width using Knuth’s rule [1]

Parameters:

data (array-like, ndim=1) – observed (one-dimensional) data
return_bins (bool (optional)) – if True, then return the bin edges

Returns:

dx (float) – optimal bin width. Bins are measured starting at the first data point.
bins (ndarray) – bin edges: returned if return_bins is True

Notes

The optimal number of bins is the value M which maximizes the function

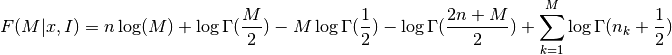
$F(M|x,I) = n\log(M) + \log\Gamma(\frac{M}{2}) - M\log\Gamma(\frac{1}{2}) - \log\Gamma(\frac{2n+M}{2}) + \sum_{k=1}^M \log\Gamma(n_k + \frac{1}{2})$

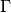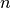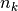where $\Gamma$ is the Gamma function, $n$ is the number of data points, $n_k$ is the number of measurements in bin $k$ .

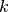References

[1]	Knuth, K.H. “Optimal Data-Based Binning for Histograms”. arXiv:0605197, 2006

hyperspy.external.astroML.histtools.scotts_bin_width(data, return_bins=False)¶

Return the optimal histogram bin width using Scott’s rule:

Parameters:

data (array-like, ndim=1) – observed (one-dimensional) data
return_bins (bool (optional)) – if True, then return the bin edges

Returns:

width (float) – optimal bin width using Scott’s rule
bins (ndarray) – bin edges: returned if return_bins is True

Notes

The optimal bin width is

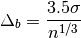
$\Delta_b = \frac{3.5\sigma}{n^{1/3}}$

where 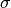$\sigma$ is the standard deviation of the data, and 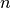$n$ is the number of data points.

See also

knuth_bin_width(), freedman_bin_width(), astroML.plotting.hist()