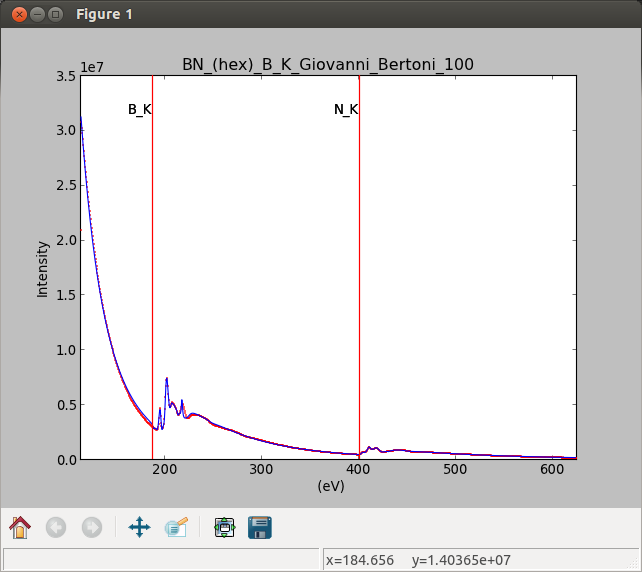
Curve fitting¶

HyperSpy can perform curve fitting in n-dimensional data sets. It can create a model from a linear combinantion of predefined components and can use multiple optimisation algorithms to fit the model to experimental data. It supports bounds and weights.

New in version 0.7: Before creating a model verify that the Signal.binned metadata attribute of the signal is set to the correct value because the resulting model depends on this parameter. See Binned and unbinned signals for more details.

Creating a model¶

A Model can be created using the create_model() method:

>>> s = hs.load('YourDataFilenameHere') # Load the data from a file
>>> m = s.create_model() # Create the model and asign it to the variable m

At this point you may be prompted to provide any necessary information not already included in the datafile, e.g.if s is EELS data, you may be asked for the accelerating voltage, convergence and collection semi-angles etc.

Adding components to the model¶

In HyperSpy a model consists of a linear combination of components. These are some of the components which are currently available:

However, this doesn’t mean that you have to limit yourself to this meagre list of function.

New in version 0.8.1: Expression component

The easiest way to turn a mathematical expression into a component is using the Expression component. For example, the following is all you need to create a`Gaussian` component with more sensible parameters for spectroscopy than the one that ships with HyperSpy:

>>> g = hs.model.components.Expression(
... expression="height * exp(-(x - x0) ** 2 * 4 * log(2)/ fwhm ** 2)",
... name="Gaussian",
... position="x0",
... height=1,
... fwhm=1,
... centre=0,
... module="numpy")

Expression uses Sympy internally to turn the string into a funtion. By default it “translates” the expression using numpy, but often it is possible to boost performance by using numexpr instead.

Expression is only useful for analytical functions. If you know how to write the function with Python, turning it into a component is very easy modifying the following template:

from hyperspy.component import Component

class My_Component(Component):

    """
    """

    def __init__(self, parameter_1=1, parameter_2=2):
        # Define the parameters
        Component.__init__(self, ('parameter_1', 'parameter_2'))

        # Optionally we can set the initial values
         self.parameter_1.value = parameter_1
         self.parameter_1.value = parameter_1

        # The units (optional)
         self.parameter_1.units = 'Tesla'
         self.parameter_2.units = 'Kociak'

        # Once defined we can give default values to the attribute is we want
        # For example we fix the attribure_1 (optional)
         self.parameter_1.attribute_1.free = False

        # And we set the boundaries (optional)
         self.parameter_1.bmin = 0.
         self.parameter_1.bmax = None

        # Optionally, to boost the optimization speed we can define also define
        # the gradients of the function we the syntax:
        # self.parameter.grad = function
         self.parameter_1.grad = self.grad_parameter_1
         self.parameter_2.grad = self.grad_parameter_2

    # Define the function as a function of the already defined parameters, x
    # being the independent variable value
    def function(self, x):
        p1 = self.parameter_1.value
        p2 = self.parameter_2.value
        return p1 + x * p2

    # Optionally define the gradients of each parameter
     def grad_parameter_1(self, x):
         """
         Returns d(function)/d(parameter_1)
         """
         return 0

     def grad_parameter_2(self, x):
         """
         Returns d(function)/d(parameter_2)
         """
         return x

If you need help with the task please submit your question to the users mailing list.

Changed in version 0.8.1: printing current model components

To print the current components in a model use components of the variable. A table with component number, attribute name, component name and component type will be printed:

>>> m
<Model, title: my signal title>
>>> m.components # an empty model
   # |            Attribute Name |            Component Name |            Component Type
---- | ------------------------- | ------------------------- | -------------------------

In fact, components may be created automatically in some cases. For example, if the Signal is recognised as EELS data, a power-law background component will automatically be placed in the model. To add a component first we have to create an instance of the component. Once the instance has been created we can add the component to the model using the append() method, e.g. for a type of data that can be modelled using gaussians we might proceed as follows:

>>> gaussian = hs.model.components.Gaussian() # Create a Gaussian function component
>>> m.append(gaussian) # Add it to the model
>>> m.components # Print the model components
   # |            Attribute Name |            Component Name |            Component Type
---- | ------------------------- | ------------------------- | -------------------------
   0 |                  Gaussian |                  Gaussian |                  Gaussian
>>> gaussian2 = hs.components.Gaussian() # Create another gaussian components
>>> gaussian3 = hs.components.Gaussian() # Create a third gaussian components

We could use the append method two times to add the two gaussians, but when adding multiple components it is handier to use the extend method that enables adding a list of components at once.

>>> m.extend((gaussian2, gaussian3)) # note the double brackets!
>>> m.components
   # |            Attribute Name |            Component Name |            Component Type
---- | ------------------------- | ------------------------- | -------------------------
   0 |                  Gaussian |                  Gaussian |                  Gaussian
   1 |                Gaussian_0 |                Gaussian_0 |                  Gaussian
   2 |                Gaussian_1 |                Gaussian_1 |                  Gaussian

We can customise the name of the components.

>>> gaussian.name = 'Carbon'
>>> gaussian2.name = 'Long Hydrogen name'
>>> gaussian3.name = 'Nitrogen'
>>> m.components
   # |            Attribute Name |            Component Name |            Component Type
---- | ------------------------- | ------------------------- | -------------------------
   0 |                    Carbon |                    Carbon |                  Gaussian
   1 |        Long_Hydrogen_name |        Long Hydrogen name |                  Gaussian
   2 |                  Nitrogen |                  Nitrogen |                  Gaussian

Two components cannot have the same name.

>>> gaussian2.name = 'Carbon'
Traceback (most recent call last):
  File "<ipython-input-5-2b5669fae54a>", line 1, in <module>
    g2.name = "Carbon"
  File "/home/fjd29/Python/hyperspy/hyperspy/component.py", line 466, in name
    "the name " + str(value))
ValueError: Another component already has the name Carbon

It is possible to access the components in the model by their name or by the index in the model.

>>> m
   # |            Attribute Name |            Component Name |            Component Type
---- | ------------------------- | ------------------------- | -------------------------
   0 |                    Carbon |                    Carbon |                  Gaussian
   1 |        Long_Hydrogen_name |        Long Hydrogen name |                  Gaussian
   2 |                  Nitrogen |                  Nitrogen |                  Gaussian
>>> m[0]
<Carbon (Gaussian component)>
>>> m["Long Hydrogen name"]
<Long Hydrogen name (Gaussian component)>

New in version 0.8.1: components attribute

In addition, the components can be accessed in the components Model attribute. This is specially useful when working in interactive data analysis with IPython because it enables tab completion.

>>> m
   # |            Attribute Name |            Component Name |            Component Type
---- | ------------------------- | ------------------------- | -------------------------
   0 |                    Carbon |                    Carbon |                  Gaussian
   1 |        Long_Hydrogen_name |        Long Hydrogen name |                  Gaussian
   2 |                  Nitrogen |                  Nitrogen |                  Gaussian
>>> m.components.Long_Hydrogen_name
<Long Hydrogen name (Gaussian component)>

It is possible to “switch off” a component by setting its active to False. When a components is switched off, to all effects it is as if it was not part of the model. To switch it on simply set the active attribute back to True.

New in version 0.7.1: active_is_multidimensional

In multidimensional signals it is possible to store the value of the active attribute at each navigation index. To enable this feature for a given component set the active_is_multidimensional attribute to True.

>>> s = hs.signals.Signal1D(np.arange(100).reshape(10,10))
>>> m = s.create_model()
>>> g1 = hs.components.Gaussian()
>>> g2 = hs.components.Gaussian()
>>> m.extend([g1,g2])
>>> g1.active_is_multidimensional = True
>>> g1._active_array
array([ True,  True,  True,  True,  True,  True,  True,  True,  True,  True], dtype=bool)
>>> g2._active_array is None
True
>>> m.set_component_active_value(False)
>>> g1._active_array
array([False, False, False, False, False, False, False, False, False, False], dtype=bool)
>>> m.set_component_active_value(True, only_current=True)
>>> g1._active_array
array([ True, False, False, False, False, False, False, False, False, False], dtype=bool)
>>> g1.active_is_multidimensional = False
>>> g1._active_array is None
True

Getting and setting parameter values and attributes¶

print_current_values() prints the value of the parameters of the components in the current coordinates.

parameters contains a list of the parameters of a component and free_parameters lists only the free parameters.

The value of a particular parameter can be accessed in the value.

If a model contains several components with the same parameters, it is possible to change them all by using set_parameters_value(). Example:

>>> s = hs.signals.Signal1D(np.arange(100).reshape(10,10))
>>> m = s.create_model()
>>> g1 = hs.model.components.Gaussian()
>>> g2 = hs.model.components.Gaussian()
>>> m.extend([g1,g2])
>>> m.set_parameters_value('A', 20)
>>> g1.A.map['values']
array([ 20.,  20.,  20.,  20.,  20.,  20.,  20.,  20.,  20.,  20.])
>>> g2.A.map['values']
array([ 20.,  20.,  20.,  20.,  20.,  20.,  20.,  20.,  20.,  20.])
>>> m.set_parameters_value('A', 40, only_current=True)
>>> g1.A.map['values']
array([ 40.,  20.,  20.,  20.,  20.,  20.,  20.,  20.,  20.,  20.])
>>> m.set_parameters_value('A',30, component_list=[g2])
>>> g2.A.map['values']
array([ 30.,  30.,  30.,  30.,  30.,  30.,  30.,  30.,  30.,  30.])
>>> g1.A.map['values']
array([ 40.,  20.,  20.,  20.,  20.,  20.,  20.,  20.,  20.,  20.])

To set the the free state of a parameter change the free attribute. To change the free state of all parameters in a component to True use set_parameters_free(), and set_parameters_not_free() for setting them to False. Specific parameter-names can also be specified by using parameter_name_list, shown in the example:

>>> g = hs.model.components.Gaussian()
>>> g.free_parameters
set([<Parameter A of Gaussian component>,
    <Parameter sigma of Gaussian component>,
    <Parameter centre of Gaussian component>])
>>> g.set_parameters_not_free()
set([])
>>> g.set_parameters_free(parameter_name_list=['A','centre'])
set([<Parameter A of Gaussian component>,
     <Parameter centre of Gaussian component>])

Similar functions exist for Model: set_parameters_free() and set_parameters_not_free(). Which sets the free states for the parameters in components in a model. Specific components and parameter-names can also be specified. For example:

>>> g1 = hs.model.components.Gaussian()
>>> g2 = hs.model.components.Gaussian()
>>> m.extend([g1,g2])
>>> m.set_parameters_not_free()
>>> g1.free_parameters
set([])
>>> g2.free_parameters
set([])
>>> m.set_parameters_free(parameter_name_list=['A'])
>>> g1.free_parameters
set([<Parameter A of Gaussian component>])
>>> g2.free_parameters
set([<Parameter A of Gaussian component>])
>>> m.set_parameters_free([g1], parameter_name_list=['sigma'])
>>> g1.free_parameters
set([<Parameter A of Gaussian component>,
     <Parameter sigma of Gaussian component>])
>>> g2.free_parameters
set([<Parameter A of Gaussian component>])

The value of a parameter can be coupled to the value of another by setting the twin attribute.

For example:

>>> gaussian.parameters # Print the parameters of the gaussian components
(A, sigma, centre)
>>> gaussian.centre.free = False # Fix the centre
>>> gaussian.free_parameters  # Print the free parameters
set([A, sigma])
>>> m.print_current_values() # Print the current value of all the free parameters
Components  Parameter       Value
Normalized Gaussian
        A   1.000000
        sigma       1.000000
Normalized Gaussian
        centre      0.000000
        A   1.000000
        sigma       1.000000
Normalized Gaussian
        A   1.000000
        sigma       1.000000
        centre      0.000000
>>> gaussian2.A.twin = gaussian3.A # Couple the A parameter of gaussian2 to the A parameter of gaussian 3
>>> gaussian2.A.value = 10 # Set the gaussian2 centre value to 10
>>> m.print_current_values()
Components  Parameter       Value
Carbon
        sigma       1.000000
        A   1.000000
        centre      0.000000
Hydrogen
        sigma       1.000000
        A   10.000000
        centre      10.000000
Nitrogen
        sigma       1.000000
        A   10.000000
        centre      0.000000

>>> gaussian3.A.value = 5 # Set the gaussian1 centre value to 5
>>> m.print_current_values()
Components  Parameter       Value
Carbon
        sigma       1.000000
        A   1.000000
        centre      0.000000
Hydrogen
        sigma       1.000000
        A   5.000000
        centre      10.000000
Nitrogen
        sigma       1.000000
        A   5.000000
        centre      0.000000

By default the coupling function is the identity function. However it is possible to set a different coupling function by setting the twin_function and twin_inverse_function attributes. For example:

>>> gaussian2.A.twin_function = lambda x: x**2
>>> gaussian2.A.twin_inverse_function = lambda x: np.sqrt(np.abs(x))
>>> gaussian2.A.value = 4
>>> m.print_current_values()
Components  Parameter       Value
Carbon
        sigma       1.000000
        A   1.000000
        centre      0.000000
Hydrogen
        sigma       1.000000
        A   4.000000
        centre      10.000000
Nitrogen
        sigma       1.000000
        A   2.000000
        centre      0.000000

>>> gaussian3.A.value = 4
>>> m.print_current_values()
Components  Parameter       Value
Carbon
        sigma       1.000000
        A   1.000000
        centre      0.000000
Hydrogen
        sigma       1.000000
        A   16.000000
        centre      10.000000
Nitrogen
        sigma       1.000000
        A   4.000000
        centre      0.000000

Fitting the model to the data¶

To fit the model to the data at the current coordinates (e.g. to fit one spectrum at a particular point in a spectrum-image) use fit().

The following table summarizes the features of the currently available optimizers:

Features of curve fitting optimizers.¶
Optimizer	Bounds	Error estimation	Method
“leastsq”	No	Yes	least squares
“mpfit”	Yes	Yes	least squares
“odr”	No	Yes	least squares
“fmin”	No	No	least squares, maximum likelihood

The following example shows how to perfom least squares with error estimation.

First we create data consisting of a line line y = a*x + b with a = 1 and b = 100 and we add white noise to it:

>>> s = hs.signals.SpectrumSimulation(
...     np.arange(100, 300))
>>> s.add_gaussian_noise(std=100)

To fit it we create a model consisting of a Polynomial component of order 1 and fit it to the data.

>>> m = s.create_model()
>>> line = hs.model.components.Polynomial(order=1)
>>> m.append(line)
>>> m.fit()

On fitting completion, the optimized value of the parameters and their estimated standard deviation are stored in the following line attributes:

>>> line.coefficients.value
(0.99246156488437653, 103.67507406125888)
>>> line.coefficients.std
(0.11771053738516088, 13.541061301257537)

When the noise is heterocedastic, only if the metadata.Signal.Noise_properties.variance attribute of the Signal1D instance is defined can the errors be estimated accurately. If the variance is not defined, the standard deviation of the parameters are still computed and stored in the std attribute by setting variance equal 1. However, the value won’t be correct unless an accurate value of the variance is defined in metadata.Signal.Noise_properties.variance. See Setting the noise properties for more information.

In the following example, we add poissonian noise to the data instead of gaussian noise and proceed to fit as in the previous example.

>>> s = hs.signals.SpectrumSimulation(
...     np.arange(300))
>>> s.add_poissonian_noise()
>>> m = s.create_model()
>>> line  = hs.model.components.Polynomial(order=1)
>>> m.append(line)
>>> m.fit()
>>> line.coefficients.value
(1.0052331707848698, -1.0723588390873573)
>>> line.coefficients.std
(0.0081710549764721901, 1.4117294994070277)

Because the noise is heterocedastic, the least squares optimizer estimation is biased. A more accurate result can be obtained by using weighted least squares instead that, although still biased for poissonian noise, is a good approximation in most cases.

>>> s.estimate_poissonian_noise_variance(expected_value=hs.signals.Signal1D(np.arange(300)))
>>> m.fit()
>>> line.coefficients.value
(1.0004224896604759, -0.46982916592391377)
>>> line.coefficients.std
(0.0055752036447948173, 0.46950832982673557)

We can use poissonian maximum likelihood estimation instead that is an unbiased estimator for poissonian noise.

>>> m.fit(fitter="fmin", method="ml")
>>> line.coefficients.value
(1.0030718094185611, -0.63590210946134107)

Problems of ill-conditioning and divergence can be ameliorated by using bounded optimization. Currently, only the “mpfit” optimizer supports bounds. In the following example a gaussian histogram is fitted using a Gaussian component using mpfit and bounds on the centre parameter.

>>> s = hs.signals.Signal(np.random.normal(loc=10, scale=0.01,
size=1e5)).get_histogram()
>>> s.metadata.Signal.binned = True
>>> m = s.create_model()
>>> g1 = hs.model.components.Gaussian()
>>> m.append(g1)
>>> g1.centre.value = 7
>>> g1.centre.bmin = 7
>>> g1.centre.bmax = 14
>>> g1.centre.bounded = True
>>> m.fit(fitter="mpfit", bounded=True)
>>> m.print_current_values()
Components  Parameter   Value
Gaussian
        sigma   0.00996345
        A   99918.7
        centre  9.99976

New in version 0.7: chi-squared and reduced chi-squared

The chi-squared, reduced chi-squared and the degrees of freedom are computed automatically when fitting. They are stored as signals, in the chisq, red_chisq and dof attributes of the model respectively. Note that, unless metadata.Signal.Noise_properties.variance contains an accurate estimation of the variance of the data, the chi-squared and reduced chi-squared cannot be computed correctly. This is also true for homocedastic noise.

Visualizing the model¶

To visualise the result use the plot() method:

>>> m.plot() # Visualise the results

New in version 0.7.

By default only the full model line is displayed in the plot. In addition, it is possible to display the individual components by calling enable_plot_components() or directly using plot():

>>> m.plot(plot_components=True) # Visualise the results

To disable this feature call disable_plot_components().

New in version 0.7.1: suspend_update() and resume_update()

By default the model plot is automatically updated when any parameter value changes. It is possible to suspend this feature with suspend_update(). To resume it use resume_update().

Setting the initial parameters¶

Non-linear regression often requires setting sensible starting parameters. This can be done by plotting the model and adjusting the parameters by hand.

New in version 0.7: In addition, it is possible to fit a given component independently using the fit_component() method.

New in version 0.8.5: notebook_interaction(),

If running in a Jupyter Notebook, interactive widgets can be used to conveniently adjust the parameter values by running notebook_interaction() for Model, Component and Parameter.

Warning

notebook_interaction() functions require ipywidgets, which is an optional dependency of HyperSpy.

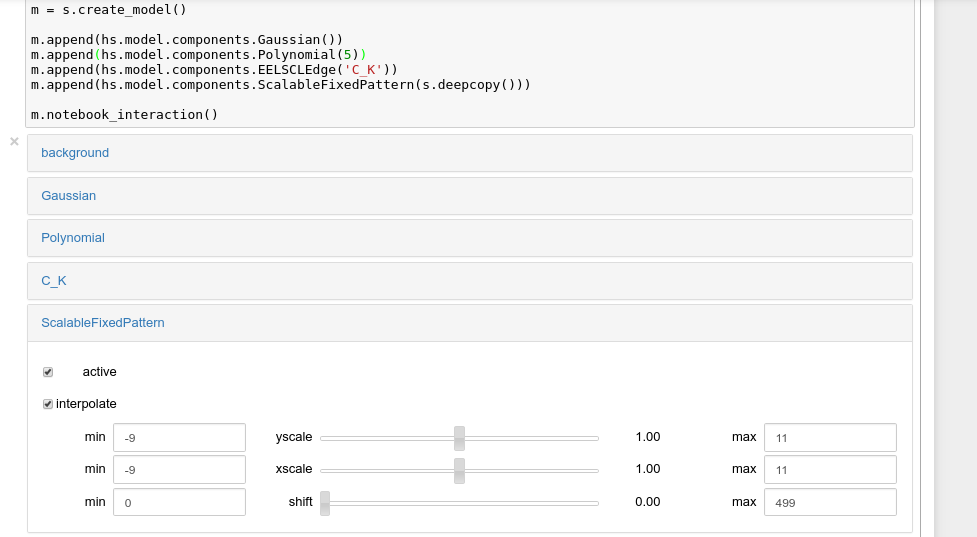
Interactive widgets for the full model in a Jupyter notebook. Drag the sliders to adjust current parameter values. Typing different minimum and maximum values changes the boundaries of the slider.

New in version 0.6: enable_adjust_position() and disable_adjust_position()

Also, enable_adjust_position() provides an interactive way of setting the position of the components with a well define position. disable_adjust_position() disables the tool.

Interactive component position adjustment tool.Drag the vertical lines to set the initial value of the position parameter.

Exclude data from the fitting process¶

The following Model methods can be used to exclude undesired spectral channels from the fitting process:

Fitting multidimensional datasets¶

To fit the model to all the elements of a multidimensional datataset use multifit(), e.g.:

>>> m.multifit() # warning: this can be a lengthy process on large datasets

multifit() fits the model at the first position, store the result of the fit internally and move to the next position until reaching the end of the dataset.

Sometimes one may like to store and fetch the value of the parameters at a given position manually. This is possible using store_current_values() and fetch_stored_values().

Visualising the result of the fit¶

The Model plot_results(), Component plot() and Parameter plot() methods can be used to visualise the result of the fit when fitting multidimensional datasets.

Saving and loading the result of the fit¶

As of HyperSpy 0.8, the following is the only way to save a model to a file and load it back. Note that this method is known to be brittle i.e. there is no guarantee that a version of HyperSpy different from the one used to save the model will be able to load it sucessfully. Also, it is advisable not to use this method in combination with functions that alter the value of the parameters interactively (e.g. enable_adjust_position) as the modifications made by this functions are normally not stored in the IPython notebook or Python script.

To save a model:

Save the parameter arrays to a file using save_parameters2file().
Save all the commands that used to create the model to a file. This can be done in the form of an IPython notebook or a Python script.
(Optional) Comment out or delete the fitting commangs (e.g. multifit).

To recreate the model:

Execute the IPython notebook or Python script.
Use load_parameters_from_file() to load back the parameter values and arrays.

Exporting the result of the fit¶

The Model export_results(), Component export() and Parameter export() methods can be used to export the result of the optimization in all supported formats.

Batch setting of parameter attributes¶

New in version 0.6.

The following methods can be used to ease the task of setting some important parameter attributes: