hyperspy._signals.eels module¶
-
class
hyperspy._signals.eels.EELSSpectrum(*args, **kwargs)¶ Bases:
hyperspy._signals.eels.EELSSpectrum_mixin,hyperspy._signals.signal1d.Signal1D
-
class
hyperspy._signals.eels.EELSSpectrum_mixin(*args, **kwargs)¶ Bases:
object-
add_elements(elements, include_pre_edges=False)¶ Declare the elemental composition of the sample.
The ionisation edges of the elements present in the current energy range will be added automatically.
- Parameters
elements (tuple of strings) – The symbol of the elements. Note this input must always be in the form of a tuple. Meaning: add_elements((‘C’,)) will work, while add_elements((‘C’)) will NOT work.
include_pre_edges (bool) – If True, the ionization edges with an onset below the lower energy limit of the SI will be incluided
Examples
>>> s = hs.signals.EELSSpectrum(np.arange(1024)) >>> s.add_elements(('C', 'O'))
- Raises
ValueError –
-
align_zero_loss_peak(calibrate=True, also_align=[], print_stats=True, subpixel=True, mask=None, signal_range=None, show_progressbar=None, crop=True, **kwargs)¶ Align the zero-loss peak.
This function first aligns the spectra using the result of estimate_zero_loss_peak_centre and afterward, if subpixel is True, proceeds to align with subpixel accuracy using align1D. The offset is automatically correct if calibrate is True.
- Parameters
calibrate (bool) – If True, set the offset of the spectral axis so that the zero-loss peak is at position zero.
also_align (list of signals) – A list containing other spectra of identical dimensions to align using the shifts applied to the current spectrum. If calibrate is True, the calibration is also applied to the spectra in the list.
print_stats (bool) – If True, print summary statistics of the ZLP maximum before the aligment.
subpixel (bool) – If True, perform the alignment with subpixel accuracy using cross-correlation.
mask (Signal1D of bool data type.) – It must have signal_dimension = 0 and navigation_shape equal to the current signal. Where mask is True the shift is not computed and set to nan.
signal_range (tuple of integers, tuple of floats. Optional) – Will only search for the ZLP within the signal_range. If given in integers, the range will be in index values. If given floats, the range will be in spectrum values. Useful if there are features in the spectrum which are more intense than the ZLP. Default is searching in the whole signal.
show_progressbar (None or bool) – If True, display a progress bar. If None the default from the preferences settings is used.
crop (bool) – If True automatically crop the signal axis at both ends if needed.
Examples
>>> s_ll = hs.signals.EELSSpectrum(np.zeros(1000)) >>> s_ll.data[100] = 100 >>> s_ll.align_zero_loss_peak()
Aligning both the lowloss signal and another signal
>>> s = hs.signals.EELSSpectrum(np.range(1000)) >>> s_ll.align_zero_loss_peak(also_align=[s])
Aligning within a narrow range of the lowloss signal
>>> s_ll.align_zero_loss_peak(signal_range=(-10.,10.))
See also
estimate_zero_loss_peak_centre(),align1D(),estimate_shift1D.()Notes
Any extra keyword arguments are passed to align1D. For more information read its docstring.
-
create_model(ll=None, auto_background=True, auto_add_edges=True, GOS=None, dictionary=None)¶ Create a model for the current EELS data.
- Parameters
ll (EELSSpectrum, optional) – If an EELSSpectrum is provided, it will be assumed that it is a low-loss EELS spectrum, and it will be used to simulate the effect of multiple scattering by convolving it with the EELS spectrum.
auto_background (boolean, default True) – If True, and if spectrum is an EELS instance adds automatically a powerlaw to the model and estimate the parameters by the two-area method.
auto_add_edges (boolean, default True) – If True, and if spectrum is an EELS instance, it will automatically add the ionization edges as defined in the Signal1D instance. Adding a new element to the spectrum using the components.EELSSpectrum.add_elements method automatically add the corresponding ionisation edges to the model.
GOS ({'hydrogenic' | 'Hartree-Slater'}, optional) – The generalized oscillation strenght calculations to use for the core-loss EELS edges. If None the Hartree-Slater GOS are used if available, otherwise it uses the hydrogenic GOS.
dictionary ({None | dict}, optional) – A dictionary to be used to recreate a model. Usually generated using
hyperspy.model.as_dictionary()
- Returns
model
- Return type
EELSModel instance.
-
estimate_elastic_scattering_intensity(threshold, show_progressbar=None)¶ Rough estimation of the elastic scattering intensity by truncation of a EELS low-loss spectrum.
- Parameters
threshold ({Signal1D, float, int}) – Truncation energy to estimate the intensity of the elastic scattering. The threshold can be provided as a signal of the same dimension as the input spectrum navigation space containing the threshold value in the energy units. Alternatively a constant threshold can be specified in energy/index units by passing float/int.
show_progressbar (None or bool) – If True, display a progress bar. If None the default from the preferences settings is used.
- Returns
I0 – The elastic scattering intensity.
- Return type
-
estimate_elastic_scattering_threshold(window=10.0, tol=None, window_length=5, polynomial_order=3, start=1.0)¶ Calculate the first inflexion point of the spectrum derivative within a window.
This method assumes that the zero-loss peak is located at position zero in all the spectra. Currently it looks for an inflexion point, that can be a local maximum or minimum. Therefore, to estimate the elastic scattering threshold start + window must be less than the first maximum for all spectra (often the bulk plasmon maximum). If there is more than one inflexion point in energy the window it selects the smoother one what, often, but not always, is a good choice in this case.
- Parameters
window ({None, float}) – If None, the search for the local inflexion point is performed using the full energy range. A positive float will restrict the search to the (0,window] energy window, where window is given in the axis units. If no inflexion point is found in this spectral range the window value is returned instead.
tol ({None, float}) – The threshold tolerance for the derivative. If “auto” it is automatically calculated as the minimum value that guarantees finding an inflexion point in all the spectra in given energy range.
window_length (int) – If non zero performs order three Savitzky-Golay smoothing to the data to avoid falling in local minima caused by the noise. It must be an odd interger.
polynomial_order (int) – Savitzky-Golay filter polynomial order.
start (float) – Position from the zero-loss peak centre from where to start looking for the inflexion point.
- Returns
threshold – A Signal1D of the same dimension as the input spectrum navigation space containing the estimated threshold. Where the threshold couldn’t be estimated the value is set to nan.
- Return type
See also
estimate_elastic_scattering_intensity(),align_zero_loss_peak(),find_peaks1D_ohaver(),fourier_ratio_deconvolution.()Notes
The main purpose of this method is to be used as input for estimate_elastic_scattering_intensity. Indeed, for currently achievable energy resolutions, there is not such a thing as a elastic scattering threshold. Therefore, please be aware of the limitations of this method when using it.
-
estimate_thickness(threshold, zlp=None)¶ Estimates the thickness (relative to the mean free path) of a sample using the log-ratio method.
The current EELS spectrum must be a low-loss spectrum containing the zero-loss peak. The hyperspectrum must be well calibrated and aligned.
- Parameters
threshold ({Signal1D, float, int}) – Truncation energy to estimate the intensity of the elastic scattering. The threshold can be provided as a signal of the same dimension as the input spectrum navigation space containing the threshold value in the energy units. Alternatively a constant threshold can be specified in energy/index units by passing float/int.
zlp ({None, EELSSpectrum}) – If not None the zero-loss peak intensity is calculated from the ZLP spectrum supplied by integration using Simpson’s rule. If None estimates the zero-loss peak intensity using estimate_elastic_scattering_intensity by truncation.
- Returns
s – The thickness relative to the MFP. It returns a Signal1D, Signal2D or a BaseSignal, depending on the current navigation dimensions.
- Return type
Notes
For details see: Egerton, R. Electron Energy-Loss Spectroscopy in the Electron Microscope. Springer-Verlag, 2011.
-
estimate_zero_loss_peak_centre(mask=None)¶ Estimate the posision of the zero-loss peak.
This function provides just a coarse estimation of the position of the zero-loss peak centre by computing the position of the maximum of the spectra. For subpixel accuracy use estimate_shift1D.
- Parameters
mask (Signal1D of bool data type.) – It must have signal_dimension = 0 and navigation_shape equal to the current signal. Where mask is True the shift is not computed and set to nan.
- Returns
zlpc – The estimated position of the maximum of the ZLP peak.
- Return type
Signal1D subclass
Notes
This function only works when the zero-loss peak is the most intense feature in the spectrum. If it is not in most cases the spectrum can be cropped to meet this criterium. Alternatively use estimate_shift1D.
See also
estimate_shift1D(),align_zero_loss_peak()
-
fourier_log_deconvolution(zlp, add_zlp=False, crop=False)¶ Performs fourier-log deconvolution.
- Parameters
zlp (EELSSpectrum) – The corresponding zero-loss peak.
add_zlp (bool) – If True, adds the ZLP to the deconvolved spectrum
crop (bool) – If True crop the spectrum to leave out the channels that have been modified to decay smoothly to zero at the sides of the spectrum.
- Returns
- Return type
An EELSSpectrum containing the current data deconvolved.
Notes
For details see: Egerton, R. Electron Energy-Loss Spectroscopy in the Electron Microscope. Springer-Verlag, 2011.
-
fourier_ratio_deconvolution(ll, fwhm=None, threshold=None, extrapolate_lowloss=True, extrapolate_coreloss=True)¶ Performs Fourier-ratio deconvolution.
- The core-loss should have the background removed. To reduce
the noise amplication the result is convolved with a
Gaussian function.
- Parameters
ll (EELSSpectrum) – The corresponding low-loss (ll) EELSSpectrum.
fwhm (float or None) – Full-width half-maximum of the Gaussian function by which the result of the deconvolution is convolved. It can be used to select the final SNR and spectral resolution. If None, the FWHM of the zero-loss peak of the low-loss is estimated and used.
threshold ({None, float}) –
Truncation energy to estimate the intensity of the elastic scattering. If None the threshold is taken as the
first minimum after the ZLP centre.
extrapolate_coreloss (extrapolate_lowloss,) – If True the signals are extrapolated using a power law,
Notes
For details see: Egerton, R. Electron Energy-Loss Spectroscopy in the Electron Microscope. Springer-Verlag, 2011.
-
generate_subshells(include_pre_edges=False)¶ Calculate the subshells for the current energy range for the elements present in self.elements
- Parameters
include_pre_edges (bool) – If True, the ionization edges with an onset below the lower energy limit of the SI will be incluided
-
kramers_kronig_analysis(zlp=None, iterations=1, n=None, t=None, delta=0.5, full_output=False)¶ Calculate the complex dielectric function from a single scattering distribution (SSD) using the Kramers-Kronig relations.
It uses the FFT method as in [Egerton2011]. The SSD is an EELSSpectrum instance containing SSD low-loss EELS with no zero-loss peak. The internal loop is devised to approximately subtract the surface plasmon contribution supposing an unoxidized planar surface and neglecting coupling between the surfaces. This method does not account for retardation effects, instrumental broading and surface plasmon excitation in particles.
Note that either refractive index or thickness are required. If both are None or if both are provided an exception is raised.
- Parameters
zlp ({None, number, Signal1D}) – ZLP intensity. It is optional (can be None) if t is None and n is not None and the thickness estimation is not required. If t is not None, the ZLP is required to perform the normalization and if t is not None, the ZLP is required to calculate the thickness. If the ZLP is the same for all spectra, the integral of the ZLP can be provided as a number. Otherwise, if the ZLP intensity is not the same for all spectra, it can be provided as i) a Signal1D of the same dimensions as the current signal containing the ZLP spectra for each location ii) a BaseSignal of signal dimension 0 and navigation_dimension equal to the current signal containing the integrated ZLP intensity.
iterations (int) – Number of the iterations for the internal loop to remove the surface plasmon contribution. If 1 the surface plasmon contribution is not estimated and subtracted (the default is 1).
n ({None, float}) – The medium refractive index. Used for normalization of the SSD to obtain the energy loss function. If given the thickness is estimated and returned. It is only required when t is None.
t ({None, number, Signal1D}) – The sample thickness in nm. Used for normalization of the SSD to obtain the energy loss function. It is only required when n is None. If the thickness is the same for all spectra it can be given by a number. Otherwise, it can be provided as a BaseSignal with signal dimension 0 and navigation_dimension equal to the current signal.
delta (float) – A small number (0.1-0.5 eV) added to the energy axis in specific steps of the calculation the surface loss correction to improve stability.
full_output (bool) – If True, return a dictionary that contains the estimated thickness if t is None and the estimated surface plasmon excitation and the spectrum corrected from surface plasmon excitations if iterations > 1.
- Returns
eps (DielectricFunction instance) –
The complex dielectric function results,
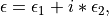
contained in an DielectricFunction instance.
output (Dictionary (optional)) – A dictionary of optional outputs with the following keys:
thicknessThe estimated thickness in nm calculated by normalization of the SSD (only when t is None)
surface plasmon estimationThe estimated surface plasmon excitation (only if iterations > 1.)
- Raises
ValuerError – If both n and t are undefined (None).
AttribureError – If the beam_energy or the collection semi-angle are not defined in metadata.
Notes
This method is based in Egerton’s Matlab code [Egerton2011] with some minor differences:
The integrals are performed using the simpsom rule instead of using a summation.
The wrap-around problem when computing the ffts is workarounded by padding the signal instead of substracting the reflected tail.
-
power_law_extrapolation(window_size=20, extrapolation_size=1024, add_noise=False, fix_neg_r=False)¶ Extrapolate the spectrum to the right using a powerlaw
- Parameters
window_size (int) – The number of channels from the right side of the spectrum that are used to estimate the power law parameters.
extrapolation_size (int) – Size of the extrapolation in number of channels
add_noise (bool) – If True, add poissonian noise to the extrapolated spectrum.
fix_neg_r (bool) – If True, the negative values for the “components.PowerLaw” parameter r will be flagged and the extrapolation will be done with a constant zero-value.
- Returns
- Return type
A new spectrum, with the extrapolation.
-
rebin(new_shape=None, scale=None, crop=True, out=None)¶ Rebin array.
Rebin the signal into a smaller or larger shape, based on linear interpolation. Specify either new_shape or scale.
- Parameters
new_shape (a list of floats or integer, default None) – For each dimension specify the new_shape. This will then be converted into a scale.
scale (a list of floats or integer, default None) – For each dimension specify the new:old pixel ratio, e.g. a ratio of 1 is no binning and a ratio of 2 means that each pixel in the new spectrum is twice the size of the pixels in the old spectrum. The length of the list should match the dimension of the numpy array. *Note : Only one of scale or new_shape should be specified otherwise the function will not run*
crop (bool, default True) –
When binning by a non-integer number of pixels it is likely that the final row in each dimension contains less than the full quota to fill one pixel.
e.g. 5*5 array binned by 2.1 will produce two rows containing 2.1 pixels and one row containing only 0.8 pixels worth. Selection of crop=’True’ or crop=’False’ determines whether or not this ‘black’ line is cropped from the final binned array or not.
Please note that if crop=False is used, the final row in each dimension may appear black, if a fractional number of pixels are left over. It can be removed but has been left to preserve total counts before and after binning.
out (Signal or None) – If None, a new Signal is created with the result of the operation and returned (default). If a Signal is passed, it is used to receive the output of the operation, and nothing is returned.
- Returns
s
- Return type
Signal subclass
Examples
>>> spectrum = hs.signals.EDSTEMSpectrum(np.ones([4, 4, 10])) >>> spectrum.data[1, 2, 9] = 5 >>> print(spectrum) <EDXTEMSpectrum, title: dimensions: (4, 4|10)> >>> print ('Sum = ', sum(sum(sum(spectrum.data)))) Sum = 164.0 >>> scale = [2, 2, 5] >>> test = spectrum.rebin(scale) >>> print(test) <EDSTEMSpectrum, title: dimensions (2, 2|2)> >>> print('Sum = ', sum(sum(sum(test.data)))) Sum = 164.0
-
richardson_lucy_deconvolution(psf, iterations=15, mask=None, show_progressbar=None, parallel=None)¶ 1D Richardson-Lucy Poissonian deconvolution of the spectrum by the given kernel.
- Parameters
iterations (int) – Number of iterations of the deconvolution. Note that increasing the value will increase the noise amplification.
psf (EELSSpectrum) – It must have the same signal dimension as the current spectrum and a spatial dimension of 0 or the same as the current spectrum.
show_progressbar (None or bool) – If True, display a progress bar. If None the default from the preferences settings is used.
parallel (None or bool) – If True, perform computation in parallel using multiple cores. If None the default from the preferences settings is used.
Notes
For details on the algorithm see Gloter, A., A. Douiri, M. Tence, and C. Colliex. “Improving Energy Resolution of EELS Spectra: An Alternative to the Monochromator Solution.” Ultramicroscopy 96, no. 3–4 (September 2003): 385–400.
-
set_microscope_parameters(beam_energy=None, convergence_angle=None, collection_angle=None, toolkit=None, display=True)¶ Set the microscope parameters that are necessary to calculate the GOS.
If not all of them are defined, in interactive mode raises an UI item to fill the values
- beam_energy: float
The energy of the electron beam in keV
- convengence_anglefloat
The microscope convergence semi-angle in mrad.
- collection_anglefloat
The collection semi-angle in mrad.
- toolkitstr, iterable of strings or None
If None (default), all available widgets are displayed or returned. If string, only the widgets of the selected toolkit are displayed if available. If an interable of toolkit strings, the widgets of all listed toolkits are displayed or returned.
- displaybool
If True, display the user interface widgets. If False, return the widgets container in a dictionary, usually for customisation or testing.
-
-
class
hyperspy._signals.eels.EELSTEMParametersUI(signal)¶ Bases:
hyperspy.signal.BaseSetMetadataItems-
gui(display=True, toolkit=None, **kwargs)¶ Display or return interactive GUI element if available.
- Parameters
display (bool) – If True, display the user interface widgets. If False, return the widgets container in a dictionary, usually for customisation or testing.
toolkit (str, iterable of strings or None) – If None (default), all available widgets are displayed or returned. If string, only the widgets of the selected toolkit are displayed if available. If an interable of toolkit strings, the widgets of all listed toolkits are displayed or returned.
-
mapping= {'Acquisition_instrument.TEM.Detector.EELS.collection_angle': 'collection_angle', 'Acquisition_instrument.TEM.beam_energy': 'beam_energy', 'Acquisition_instrument.TEM.convergence_angle': 'convergence_angle'}¶
-
-
class
hyperspy._signals.eels.LazyEELSSpectrum(*args, **kwargs)¶ Bases:
hyperspy._signals.eels.EELSSpectrum,hyperspy._signals.signal1d.LazySignal1D