Model fitting

HyperSpy can perform curve fitting of one-dimensional signals (spectra) and two-dimensional signals (images) in n-dimensional data sets. Models can be created as a linear combination of predefined components and multiple optimisation algorithms can be used to fit the model to experimental data. Bounds and weights are supported. The syntax for creating both kinds of model is essentially the same, as in this documentation any method referred to in the BaseModel class is available for both kinds.

2D models. Note that this first implementation lacks many of the features of 1D models e.g. plotting. Those will be added in future releases.

Models can be created and fit to experimental data in both one and two dimensions i.e. spectra and images respectively. Most of the syntax is identical in either case. A one-dimensional model is created when a model is created for a Signal1D whereas a two- dimensional model is created for a Signal2D. At present plotting and gradient fitting methods tools for are not yet provided for the Model2D class.

Binned/unbinned signals

Before creating a model verify that the Signal.binned metadata attribute of the signal is set to the correct value because the resulting model depends on this parameter. See Binned and unbinned signals for more details.

Warning

When importing data that have been binned using other software, in particular Gatan’s DM, the stored values may be the averages of the binned channels or pixels, instead of their sum, as would be required for proper statistical analysis. We therefore cannot guarantee that the statistics will be valid. We therefore strongly recommend that all pre-fitting binning should be done using Hyperspy.

Creating a model

A Model1D can be created for data in the Signal1D class using the create_model() method:

>>> s = hs.signals.Signal1D(np.arange(300).reshape(30, 10))
>>> m = s.create_model() # Creates the 1D-Model and assign it to m

Similarly A Model2D can be created for data in the Signal2D class using the create_model() method:

>>> im = hs.signals.Signal2D(np.arange(300).reshape(3, 10, 10))
>>> mod = im.create_model() # Create the 2D-Model and assign it to mod

The syntax for creating both one-dimensional and two-dimensional models is thus identical for the user in practice. When a model is created you may be prompted to provide important information not already included in the datafile, e.g.if s is EELS data, you may be asked for the accelerating voltage, convergence and collection semi-angles etc.

Creating components for the model

In HyperSpy a model consists of a linear combination of components and various components are available in one (components1d)and two-dimensions (components2d) to construct a model.

The following components are currently available for one-dimensional models:

• EELSCLEdge

• VolumePlasmonDrude

• PowerLaw

• Offset

• Exponential

• Expression

• ScalableFixedPattern

• Gaussian

• GaussianHF

• Lorentzian

• Voigt

• Polynomial

• Logistic

• Bleasdale

• Erf

• SEE

• Arctan

• HeavisideStep

The following components are currently available for two-dimensional models:

• Gaussian2D

• Expression

However, this doesn’t mean that you have to limit yourself to this meagre list of functions. A new function can easily be written as specified as below.

Specifying custom components

New in version 1.2: Expression component can create 2D components.

The easiest way to turn a mathematical expression into a component is using the Expression component. For example, the following is all you need to create a Gaussian component with more sensible parameters for spectroscopy than the one that ships with HyperSpy:

>>> g = hs.model.components1D.Expression(
... expression="height * exp(-(x - x0) ** 2 * 4 * log(2)/ fwhm ** 2)",
... name="Gaussian",
... position="x0",
... height=1,
... fwhm=1,
... x0=0,
... module="numpy")

If the expression is inconvenient to write out in full (e.g. it’s long and/or complicated), multiple substitutions can be given, separated by semicolons. Both symbolic and numerical substitutions are allowed:

>>> expression = "h / sqrt(p2) ; p2 = 2 * m0 * e1 * x * brackets;"
>>> expression += "brackets = 1 + (e1 * x) / (2 * m0 * c * c) ;"
>>> expression += "m0 = 9.1e-31 ; c = 3e8; e1 = 1.6e-19 ; h = 6.6e-34"
>>> wavelength = hs.model.components1D.Expression(
... expression=expression,
... name="Electron wavelength with voltage")

Expression uses Sympy internally to turn the string into a function. By default it “translates” the expression using numpy, but often it is possible to boost performance by using numexpr instead.

It can also create 2D components with optional rotation. In the following example we create a 2D gaussian that rotates around its center:

>>> g = hs.model.components2D.Expression(
... "k * exp(-((x-x0)**2 / (2 * sx ** 2) + (y-y0)**2 / (2 * sy ** 2)))",
... "Gaussian2d", add_rotation=True, position=("x0", "y0"),
... module="numpy", )

Of course Expression is only useful for analytical functions. For more general components you need to create the component “by hand”. The good news is that, if you know how to write the function with Python, turning it into a component is very easy, just modify the following template to suit your needs:

from hyperspy.component import Component

class MyComponent(Component):

    """
    """

    def __init__(self, parameter_1=1, parameter_2=2):
        # Define the parameters
        Component.__init__(self, ('parameter_1', 'parameter_2'))

        # Optionally we can set the initial values
        self.parameter_1.value = parameter_1
        self.parameter_1.value = parameter_1

        # The units (optional)
        self.parameter_1.units = 'Tesla'
        self.parameter_2.units = 'Kociak'

        # Once defined we can give default values to the attribute
        # For example we fix the attribure_1 (optional)
        self.parameter_1.attribute_1.free = False

        # And we set the boundaries (optional)
        self.parameter_1.bmin = 0.
        self.parameter_1.bmax = None

        # Optionally, to boost the optimization speed we can also define
        # the gradients of the function we the syntax:
        # self.parameter.grad = function
        self.parameter_1.grad = self.grad_parameter_1
        self.parameter_2.grad = self.grad_parameter_2

    # Define the function as a function of the already defined parameters,
    # x being the independent variable value
    def function(self, x):
        p1 = self.parameter_1.value
        p2 = self.parameter_2.value
        return p1 + x * p2

    # Optionally define the gradients of each parameter
    def grad_parameter_1(self, x):
        """
        Returns d(function)/d(parameter_1)
        """
        return 0

    def grad_parameter_2(self, x):
        """
        Returns d(function)/d(parameter_2)
        """
        return x

If you need help with the task please submit your question to the users mailing list.

Adding components to the model

To print the current components in a model use components. A table with component number, attribute name, component name and component type will be printed:

>>> m
<Model, title: my signal title>
>>> m.components # an empty model
   # |       Attribute Name |       Component Name |        Component Type
---- | -------------------- | -------------------- | ---------------------

In fact, components may be created automatically in some cases. For example, if the Signal1D is recognised as EELS data, a power-law background component will automatically be placed in the model. To add a component, first we have to create an instance of the component. Once the instance has been created we can add the component to the model using the append() and extend() methods for one or more components respectively. As an example for a type of data that can be modelled using Gaussians we might proceed as follows:

>>> gaussian = hs.model.components1D.Gaussian() # Create a Gaussian comp.
>>> m.append(gaussian) # Add it to the model
>>> m.components # Print the model components
   # |       Attribute Name |        Component Name |        Component Type
---- | -------------------- | --------------------- | ---------------------
   0 |             Gaussian |              Gaussian |              Gaussian
>>> gaussian2 = hs.model.components1D.Gaussian() # Create another gaussian
>>> gaussian3 = hs.model.components1D.Gaussian() # Create a third gaussian

We could use the append() method twice to add the two gaussians, but when adding multiple components it is handier to use the extend method that enables adding a list of components at once.

>>> m.extend((gaussian2, gaussian3)) # note the double parentheses!
>>> m.components
   # |       Attribute Name |      Component Name |        Component Type
---- | -------------------- | ------------------- | ---------------------
   0 |             Gaussian |            Gaussian |              Gaussian
   1 |           Gaussian_0 |          Gaussian_0 |              Gaussian
   2 |           Gaussian_1 |          Gaussian_1 |              Gaussian

We can customise the name of the components.

>>> gaussian.name = 'Carbon'
>>> gaussian2.name = 'Long Hydrogen name'
>>> gaussian3.name = 'Nitrogen'
>>> m.components
   # |        Attribute Name |        Component Name |      Component Type
---- | --------------------- | --------------------- | -------------------
   0 |                Carbon |                Carbon |            Gaussian
   1 |    Long_Hydrogen_name |    Long Hydrogen name |            Gaussian
   2 |              Nitrogen |              Nitrogen |            Gaussian

Two components cannot have the same name.

>>> gaussian2.name = 'Carbon'
Traceback (most recent call last):
  File "<ipython-input-5-2b5669fae54a>", line 1, in <module>
    g2.name = "Carbon"
  File "/home/fjd29/Python/hyperspy/hyperspy/component.py", line 466, in
    name "the name " + str(value))
ValueError: Another component already has the name Carbon

It is possible to access the components in the model by their name or by the index in the model.

>>> m
   # |        Attribute Name |       Component Name |      Component Type
---- | --------------------- | -------------------- | -------------------
   0 |                Carbon |               Carbon |            Gaussian
   1 |    Long_Hydrogen_name |   Long Hydrogen name |            Gaussian
   2 |              Nitrogen |             Nitrogen |            Gaussian
>>> m[0]
<Carbon (Gaussian component)>
>>> m["Long Hydrogen name"]
<Long Hydrogen name (Gaussian component)>

In addition, the components can be accessed in the components Model attribute. This is specially useful when working in interactive data analysis with IPython because it enables tab completion.

>>> m
   # |        Attribute Name |        Component Name |      Component Type
---- | --------------------- | --------------------- | -------------------
   0 |                Carbon |                Carbon |            Gaussian
   1 |    Long_Hydrogen_name |    Long Hydrogen name |            Gaussian
   2 |              Nitrogen |              Nitrogen |            Gaussian
>>> m.components.Long_Hydrogen_name
<Long Hydrogen name (Gaussian component)>

It is possible to “switch off” a component by setting its active attribute to False. When a component is switched off, to all effects it is as if it was not part of the model. To switch it on simply set the active attribute back to True.

In multidimensional signals it is possible to store the value of the active attribute at each navigation index. To enable this feature for a given component set the active_is_multidimensional attribute to True.

>>> s = hs.signals.Signal1D(np.arange(100).reshape(10,10))
>>> m = s.create_model()
>>> g1 = hs.model.components1D.Gaussian()
>>> g2 = hs.model.components1D.Gaussian()
>>> m.extend([g1,g2])
>>> g1.active_is_multidimensional = True
>>> g1._active_array
array([ True,  True,  True,  True,  True,  True,  True,  True,  True,  True], dtype=bool)
>>> g2._active_array is None
True
>>> m.set_component_active_value(False)
>>> g1._active_array
array([False, False, False, False, False, False, False, False, False, False], dtype=bool)
>>> m.set_component_active_value(True, only_current=True)
>>> g1._active_array
array([ True, False, False, False, False, False, False, False, False, False], dtype=bool)
>>> g1.active_is_multidimensional = False
>>> g1._active_array is None
True

Indexing the model

Often it is useful to consider only part of the model - for example at a particular location (i.e. a slice in the navigation space) or energy range (i.e. a slice in the signal space). This can be done using exactly the same syntax that we use for signal indexing (Indexing). red_chisq and dof are automatically recomputed for the resulting slices.

>>> s = hs.signals.Signal1D(np.arange(100).reshape(10,10))
>>> m = s.create_model()
>>> m.append(hs.model.components1D.Gaussian())
>>> # select first three navigation pixels and last five signal channels
>>> m1 = m.inav[:3].isig[-5:]
>>> m1.signal
<Signal1D, title: , dimensions: (3|5)>

Getting and setting parameter values and attributes

print_current_values() prints the value of the parameters of the components in the current coordinates.

The current coordinates can be either set by navigating the plot(), or specified by pixel indices in m.axes_manager.indices or as calibrated coordinates in m.axes_manager.coordinates.

parameters contains a list of the parameters of a component and free_parameters lists only the free parameters.

The value of a particular parameter in the current coordinates can be accessed by component.Parameter.value (e.g. Gaussian.A.value). To access an array of the value of the parameter across all navigation pixels, component.Parameter.map['values'] (e.g. Gaussian.A.map["values"]) can be used. On its own, component.Parameter.map returns a NumPy array with three elements: 'values', 'std' and 'is_set'. The first two give the value and standard error for each index. The last element shows whether the value has been set in a given index, either by a fitting procedure or manually.

If a model contains several components with the same parameters, it is possible to change them all by using set_parameters_value(). Example:

>>> s = hs.signals.Signal1D(np.arange(100).reshape(10,10))
>>> m = s.create_model()
>>> g1 = hs.model.components1D.Gaussian()
>>> g2 = hs.model.components1D.Gaussian()
>>> m.extend([g1,g2])
>>> m.set_parameters_value('A', 20)
>>> g1.A.map['values']
array([ 20.,  20.,  20.,  20.,  20.,  20.,  20.,  20.,  20.,  20.])
>>> g2.A.map['values']
array([ 20.,  20.,  20.,  20.,  20.,  20.,  20.,  20.,  20.,  20.])
>>> m.set_parameters_value('A', 40, only_current=True)
>>> g1.A.map['values']
array([ 40.,  20.,  20.,  20.,  20.,  20.,  20.,  20.,  20.,  20.])
>>> m.set_parameters_value('A',30, component_list=[g2])
>>> g2.A.map['values']
array([ 30.,  30.,  30.,  30.,  30.,  30.,  30.,  30.,  30.,  30.])
>>> g1.A.map['values']
array([ 40.,  20.,  20.,  20.,  20.,  20.,  20.,  20.,  20.,  20.])

To set the free state of a parameter change the free attribute. To change the free state of all parameters in a component to True use set_parameters_free(), and set_parameters_not_free() for setting them to False. Specific parameter-names can also be specified by using parameter_name_list, shown in the example:

>>> g = hs.model.components1D.Gaussian()
>>> g.free_parameters
set([<Parameter A of Gaussian component>,
    <Parameter sigma of Gaussian component>,
    <Parameter centre of Gaussian component>])
>>> g.set_parameters_not_free()
set([])
>>> g.set_parameters_free(parameter_name_list=['A','centre'])
set([<Parameter A of Gaussian component>,
     <Parameter centre of Gaussian component>])

Similar functions exist for BaseModel: set_parameters_free() and set_parameters_not_free(). Which sets the free states for the parameters in components in a model. Specific components and parameter-names can also be specified. For example:

>>> g1 = hs.model.components1D.Gaussian()
>>> g2 = hs.model.components1D.Gaussian()
>>> m.extend([g1,g2])
>>> m.set_parameters_not_free()
>>> g1.free_parameters
set([])
>>> g2.free_parameters
set([])
>>> m.set_parameters_free(parameter_name_list=['A'])
>>> g1.free_parameters
set([<Parameter A of Gaussian component>])
>>> g2.free_parameters
set([<Parameter A of Gaussian component>])
>>> m.set_parameters_free([g1], parameter_name_list=['sigma'])
>>> g1.free_parameters
set([<Parameter A of Gaussian component>,
     <Parameter sigma of Gaussian component>])
>>> g2.free_parameters
set([<Parameter A of Gaussian component>])

The value of a parameter can be coupled to the value of another by setting the twin attribute.

For example:

>>> gaussian.parameters # Print the parameters of the gaussian components
(A, sigma, centre)
>>> gaussian.centre.free = False # Fix the centre
>>> gaussian.free_parameters  # Print the free parameters
set([A, sigma])
>>> m.print_current_values() # Print the current value of all free param.
Components  Parameter       Value
Normalized Gaussian
        A   1.000000
        sigma       1.000000
Normalized Gaussian
        centre      0.000000
        A   1.000000
        sigma       1.000000
Normalized Gaussian
        A   1.000000
        sigma       1.000000
        centre      0.000000
>>> # Couple the A parameter of gaussian2 to the A parameter of gaussian 3:
>>> gaussian2.A.twin = gaussian3.A
>>> gaussian2.A.value = 10 # Set the gaussian2 centre value to 10
>>> m.print_current_values()
Components  Parameter       Value
Carbon
        sigma       1.000000
        A   1.000000
        centre      0.000000
Hydrogen
        sigma       1.000000
        A   10.000000
        centre      10.000000
Nitrogen
        sigma       1.000000
        A   10.000000
        centre      0.000000

>>> gaussian3.A.value = 5 # Set the gaussian1 centre value to 5
>>> m.print_current_values()
Components  Parameter       Value
Carbon
        sigma       1.000000
        A   1.000000
        centre      0.000000
Hydrogen
        sigma       1.000000
        A   5.000000
        centre      10.000000
Nitrogen
        sigma       1.000000
        A   5.000000
        centre      0.000000

Deprecated since version 1.2.0: Setting the twin_function and twin_inverse_function attributes. Set the twin_function_expr and twin_inverse_function_expr attributes instead.

New in version 1.2.0: twin_function_expr and twin_inverse_function_expr.

By default the coupling function is the identity function. However it is possible to set a different coupling function by setting the twin_function_expr and twin_inverse_function_expr attributes. For example:

>>> gaussian2.A.twin_function_expr = "x**2"
>>> gaussian2.A.twin_inverse_function_expr = "sqrt(abs(x))"
>>> gaussian2.A.value = 4
>>> m.print_current_values()
Components  Parameter       Value
Carbon
        sigma       1.000000
        A   1.000000
        centre      0.000000
Hydrogen
        sigma       1.000000
        A   4.000000
        centre      10.000000
Nitrogen
        sigma       1.000000
        A   2.000000
        centre      0.000000

>>> gaussian3.A.value = 4
>>> m.print_current_values()
Components  Parameter       Value
Carbon
        sigma       1.000000
        A   1.000000
        centre      0.000000
Hydrogen
        sigma       1.000000
        A   16.000000
        centre      10.000000
Nitrogen
        sigma       1.000000
        A   4.000000
        centre      0.000000

Fitting the model to the data

To fit the model to the data at the current coordinates (e.g. to fit one spectrum at a particular point in a spectrum-image) use fit().

The following table summarizes the features of the currently available optimizers. For more information on the local and global optimization algorithms, see the Scipy documentation.

New in version 1.1: Global optimizer Differential Evolution added.

Changed in version 1.1: leastsq supports bound constraints. fmin_XXX methods changed to the scipy.optimze.minimize() notation.

Features of curve fitting optimizers.

Optimizer	Bounds	Error estimation	Method	Type
“leastsq”	Yes	Yes	‘ls’	local
“mpfit”	Yes	Yes	‘ls’	local
“odr”	No	Yes	‘ls’	local
“Nelder-Mead”	No	No	‘ls’, ‘ml’, ‘custom’	local
“Powell”	No	No	‘ls’, ‘ml’, ‘custom’	local
“CG”	No	No	‘ls’, ‘ml’, ‘custom’	local
“BFGS”	No	No	‘ls’, ‘ml’, ‘custom’	local
“Newton-CG”	No	No	‘ls’, ‘ml’, ‘custom’	local
“L-BFGS-B”	Yes	No	‘ls’, ‘ml’, ‘custom’	local
“TNC”	Yes	No	‘ls’, ‘ml’, ‘custom’	local
“Differential Evolution”	Yes	No	‘ls’, ‘ml’, ‘custom’	global

Least squares with error estimation

The following example shows how to perfom least squares optimisation with error estimation.

First we create data consisting of a line line y = a*x + b with a = 1 and b = 100 and we add white noise to it:

>>> s = hs.signals.Signal1D(
...     np.arange(100, 300))
>>> s.add_gaussian_noise(std=100)

To fit it we create a model consisting of a Polynomial component of order 1 and fit it to the data.

>>> m = s.create_model()
>>> line = hs.model.components1D.Polynomial(order=1)
>>> m.append(line)
>>> m.fit()

On fitting completion, the optimized value of the parameters and their estimated standard deviation are stored in the following line attributes:

>>> line.coefficients.value
(0.99246156488437653, 103.67507406125888)
>>> line.coefficients.std
(0.11771053738516088, 13.541061301257537)

When the noise is heterocedastic, only if the metadata.Signal.Noise_properties.variance attribute of the Signal1D instance is defined can the errors be estimated accurately. If the variance is not defined, the standard deviation of the parameters are still computed and stored in the std attribute by setting variance equal 1. However, the value won’t be correct unless an accurate value of the variance is defined in metadata.Signal.Noise_properties.variance. See Setting the noise properties for more information.

Weighted least squares with error estimation

In the following example, we add poissonian noise to the data instead of gaussian noise and proceed to fit as in the previous example.

>>> s = hs.signals.Signal1D(
...     np.arange(300))
>>> s.add_poissonian_noise()
>>> m = s.create_model()
>>> line  = hs.model.components1D.Polynomial(order=1)
>>> m.append(line)
>>> m.fit()
>>> line.coefficients.value
(1.0052331707848698, -1.0723588390873573)
>>> line.coefficients.std
(0.0081710549764721901, 1.4117294994070277)

Because the noise is heterocedastic, the least squares optimizer estimation is biased. A more accurate result can be obtained by using weighted least squares instead that, although still biased for poissonian noise, is a good approximation in most cases.

>>> s.estimate_poissonian_noise_variance(
...     expected_value=hs.signals.Signal1D(np.arange(300)))
>>> m.fit()
>>> line.coefficients.value
(1.0004224896604759, -0.46982916592391377)
>>> line.coefficients.std
(0.0055752036447948173, 0.46950832982673557)

Maximum likelihood optimisation

We can use Poisson maximum likelihood estimation instead, which is an unbiased estimator for poissonian noise. To do so, we use a general optimizer called “Nelder-Mead”.

>>> m.fit(fitter="Nelder-Mead", method="ml")
>>> line.coefficients.value
(1.0030718094185611, -0.63590210946134107)

Custom optimisations

New in version 1.4: Custom optimiser functions

Instead of the in-built least squares ('ls') and maximum likelihood ('ml') optimisation functions, a custom function can be passed to the model:

>>> def my_custom_function(model, values, data, weights=None):
...    """
...    Parameters
...    ----------
...    model : Model instance
...        the model that is fitted.
...    values : np.ndarray
...        A one-dimensional array with free parameter values suggested by the
...        optimiser (that are not yet stored in the model).
...    data : np.ndarray
...        A one-dimensional array with current data that is being fitted.
...    weights : {np.ndarray, None}
...        An optional one-dimensional array with parameter weights.
...
...    Returns
...    -------
...    score : float
...        A signle float value, representing a score of the fit, with
...        lower values corresponding to better fits.
...    """
...    # Almost any operation can be performed, for example:
...    # First we store the suggested values in the model
...    model.fetch_values_from_array(values)
...
...    # Evaluate the current model
...    cur_value = model(onlyactive=True)
...
...    # Calculate the weighted difference with data
...    if weights is None:
...        weights = 1
...    difference = (data - cur_value) * weights
...
...    # Return squared and summed weighted difference
...    return (difference**2).sum()
>>> m.fit(fitter='TNC', method='custom', min_function=my_custom_function)

If the optimiser requires a gradient estimation function, it can be similarly passed, using the following signature:

>>> def my_custom_gradient_function(model, values, data, weights=None):
...    """
...    Parameters
...    ----------
...    model : Model instance
...        the model that is fitted.
...    values : np.ndarray
...        A one-dimensional array with free parameter values suggested by the
...        optimiser (that are not yet stored in the model).
...    data : np.ndarray
...        A one-dimensional array with current data that is being fitted.
...    weights : {np.ndarray, None}
...        An optional one-dimensional array with parameter weights.
...
...    Returns
...    -------
...    gradients : np.ndarray
...        a one-dimensional array of gradients, the size of `values`,
...        containing each parameter gradient with the given values
...    """
...    # As an example, estimate maximum likelihood gradient:
...    model.fetch_values_from_array(values)
...    cur_value = model(onlyactive=True)
...
...    # We use in-built jacobian estimation
...    jac = model._jacobian(values, data)
...
...    return -(jac * (data / cur_value - 1)).sum(1)
>>> m.fit(method='custom',
...       grad=True,
...       fitter='BFGS', # an optimiser that requires gradient estimation
...       min_function=my_custom_function,
...       min_function_grad=my_custom_gradient_function)

Bounded optimisation

Problems of ill-conditioning and divergence can be improved by using bounded optimization. All components’ parameters have the attributes parameter.bmin and parameter.bmax (“bounded min” and “bounded max”). When fitting using the bounded=True argument by m.fit(bounded=True) or m.multifit(bounded=True), these attributes set the minimum and maximum values allowed for parameter.value.

Currently, not all optimizers support bounds - see the table above. In the following example a gaussian histogram is fitted using a Gaussian component using mpfit and bounds on the centre parameter.

>>> s = hs.signals.BaseSignal(np.random.normal(loc=10, scale=0.01,
... size=1e5)).get_histogram()
>>> s.metadata.Signal.binned = True
>>> m = s.create_model()
>>> g1 = hs.model.components1D.Gaussian()
>>> m.append(g1)
>>> g1.centre.value = 7
>>> g1.centre.bmin = 7
>>> g1.centre.bmax = 14
>>> g1.centre.bounded = True
>>> m.fit(fitter="mpfit", bounded=True)
>>> m.print_current_values()
Components  Parameter   Value
Gaussian
        sigma   0.00996345
        A   99918.7
        centre  9.99976

Goodness of fit

The chi-squared, reduced chi-squared and the degrees of freedom are computed automatically when fitting. They are stored as signals, in the chisq, red_chisq and dof attributes of the model respectively. Note that, unless metadata.Signal.Noise_properties.variance contains an accurate estimation of the variance of the data, the chi-squared and reduced chi-squared cannot be computed correctly. This is also true for homocedastic noise.

Visualizing the model

To visualise the result use the plot() method:

>>> m.plot() # Visualise the results

By default only the full model line is displayed in the plot. In addition, it is possible to display the individual components by calling enable_plot_components() or directly using plot():

>>> m.plot(plot_components=True) # Visualise the results

To disable this feature call disable_plot_components().

New in version 1.4: Signal1D.plot keyword arguments

All extra keyword argments are passes to the plot() method of the corresponing signal object. For example, the following plots the model signal figure but not its navigator:

>>> m.plot(navigator=False)

By default the model plot is automatically updated when any parameter value changes. It is possible to suspend this feature with suspend_update().

Setting the initial parameters

Non-linear regression often requires setting sensible starting parameters. This can be done by plotting the model and adjusting the parameters by hand.

Changed in version 1.3: All notebook_interaction() methods renamed to gui(). The notebook_interaction() methods will be removed in 2.0

If running in a Jupyter Notebook, interactive widgets can be used to conveniently adjust the parameter values by running gui() for BaseModel, Component and Parameter.

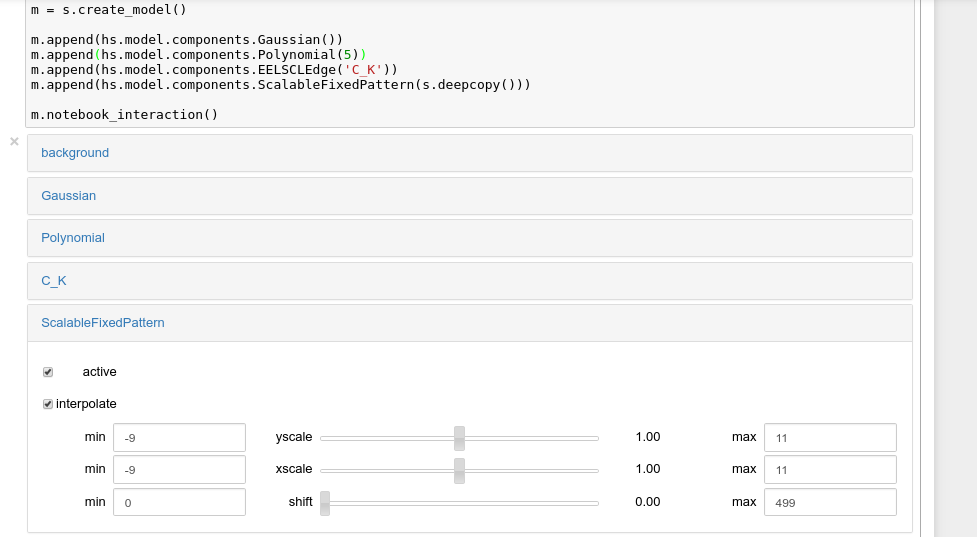
Interactive widgets for the full model in a Jupyter notebook. Drag the sliders to adjust current parameter values. Typing different minimum and maximum values changes the boundaries of the slider.

Also, enable_adjust_position() provides an interactive way of setting the position of the components with a well-defined position. disable_adjust_position() disables the tool.

Interactive component position adjustment tool. Drag the vertical lines to set the initial value of the position parameter.

Exclude data from the fitting process

The following BaseModel methods can be used to exclude undesired spectral channels from the fitting process:

• set_signal_range()

• remove_signal_range()

• reset_signal_range()

Fitting multidimensional datasets

To fit the model to all the elements of a multidimensional dataset use multifit(), e.g.:

>>> m.multifit() # warning: this can be a lengthy process on large datasets

multifit() fits the model at the first position, store the result of the fit internally and move to the next position until reaching the end of the dataset.

Note

Sometimes this method can fail, especially in the case of a TEM spectrum image of a particle surrounded by vacuum (since in that case the top-left pixel will typically be an empty signal). To get sensible starting parameters, you can do a single fit() after changing the active position within the spectrum image (either using the plotting GUI or by directly modifying s.axes_manager.indices as in Setting axis properties). After doing this, you can initialize the model at every pixel to the values from the single pixel fit using m.assign_current_values_to_all(), and then use multifit() to perform the fit over the entire spectrum image.

Sometimes one may like to store and fetch the value of the parameters at a given position manually. This is possible using store_current_values() and fetch_stored_values().

Visualising the result of the fit

The BaseModel plot_results(), Component plot() and Parameter plot() methods can be used to visualise the result of the fit when fitting multidimensional datasets.

Storing models

Multiple models can be stored in the same signal. In particular, when store() is called, a full “frozen” copy of the model is stored in stored in the signal’s ModelManager, which can be accessed in the models attribute (i.e. s.models) The stored models can be recreated at any time by calling restore() with the stored model name as an argument. To remove a model from storage, simply call remove().

The stored models can be either given a name, or assigned one automatically. The automatic naming follows alphabetical scheme, with the sequence being (a, b, …, z, aa, ab, …, az, ba, …).

Note

If you want to slice a model, you have to perform the operation on the model itself, not its stored version

Warning

Modifying a signal in-place (e.g. map(), crop(), align1D(), align2D() and similar) will invalidate all stored models. This is done intentionally.

Current stored models can be listed by calling s.models:

>>> m = s.create_model()
>>> m.append(hs.model.components1D.Lorentzian())
>>> m.store('myname')
>>> s.models
└── myname
    ├── components
    │   └── Lorentzian
    ├── date = 2015-09-07 12:01:50
    └── dimensions = (|100)

>>> m.append(hs.model.components1D.Exponential())
>>> m.store() # assign model name automatically
>>> s.models
├── a
│   ├── components
│   │   ├── Exponential
│   │   └── Lorentzian
│   ├── date = 2015-09-07 12:01:57
│   └── dimensions = (|100)
└── myname
    ├── components
    │   └── Lorentzian
    ├── date = 2015-09-07 12:01:50
    └── dimensions = (|100)
>>> m1 = s.models.restore('myname')
>>> m1.components
   # |      Attribute Name |       Component Name |       Component Type
---- | ------------------- | -------------------- | --------------------
   0 |          Lorentzian |           Lorentzian |           Lorentzian

Saving and loading the result of the fit

To save a model, a convenience function save() is provided, which stores the current model into its signal and saves the signal. As described in Storing models, more than just one model can be saved with one signal.

>>> m = s.create_model()
>>> # analysis and fitting goes here
>>> m.save('my_filename', 'model_name')
>>> l = hs.load('my_filename.hspy')
>>> m = l.models.restore('model_name') # or l.models.model_name.restore()

For older versions of HyperSpy (before 0.9), the instructions were as follows:

Note that this method is known to be brittle i.e. there is no guarantee that a version of HyperSpy different from the one used to save the model will be able to load it successfully. Also, it is advisable not to use this method in combination with functions that alter the value of the parameters interactively (e.g. enable_adjust_position) as the modifications made by this functions are normally not stored in the IPython notebook or Python script.

To save a model:

1. Save the parameter arrays to a file using save_parameters2file().

2. Save all the commands that used to create the model to a file. This can be done in the form of an IPython notebook or a Python script.

3. (Optional) Comment out or delete the fitting commands (e.g. multifit()).

To recreate the model:

1. Execute the IPython notebook or Python script.

2. Use load_parameters_from_file() to load back the parameter values and arrays.

Exporting the result of the fit

The BaseModel export_results(), Component export() and Parameter export() methods can be used to export the result of the optimization in all supported formats.

Batch setting of parameter attributes

The following model methods can be used to ease the task of setting some important parameter attributes. These can also be used on a per-component basis, by calling them on individual components.

• set_parameters_not_free()

• set_parameters_free()

• set_parameters_value()

Smart Adaptive Multi-dimensional Fitting (SAMFire)

SAMFire (Smart Adaptive Multi-dimensional Fitting) is an algorithm created to reduce the starting value (or local / false minima) problem, which often arises when fitting multi-dimensional datasets.

The algorithm will be described in full when accompanying paper is published, but we are making the implementation available now, with additional details available in the following conference proceeding.

The idea

The main idea of SAMFire is to change two things compared to the traditional way of fitting datasets with many dimensions in the navigation space:

1. Pick a more sensible pixel fitting order.

2. Calculate the pixel starting parameters from already fitted parts of the dataset.

Both of these aspects are linked one to another and are represented by two different strategy families that SAMFfire uses while operating.

Strategies

During operation SAMFire uses a list of strategies to determine how to select the next pixel and estimate its starting parameters. Only one strategy is used at a time. Next strategy is chosen when no new pixels are can be fitted with the current strategy. Once either the strategy list is exhausted or the full dataset fitted, the algorithm terminates.

There are two families of strategies. In each family there may be many strategies, using different statistical or significance measures.

As a rule of thumb, the first strategy in the list should always be from the local family, followed by a strategy from the global family.

Local strategy family

These strategies assume that locally neighbouring pixels are similar. As a result, the pixel fitting order seems to follow data-suggested order, and the starting values are computed from the surrounding already fitted pixels.

More information about the exact procedure will be available once the accompanying paper is published.

Global strategy family

Global strategies assume that the navigation coordinates of each pixel bear no relation to it’s signal (i.e. the location of pixels is meaningless). As a result, the pixels are selected at random to ensure uniform sampling of the navigation space.

A number of candidate starting values are computed form global statistical measures. These values are all attempted in order until a satisfactory result is found (not necessarily testing all available starting guesses). As a result, on average each pixel requires significantly more computations when compared to a local strategy.

More information about the exact procedure will be available once the accompanying paper is published.

Seed points

Due to the strategies using already fitted pixels to estimate the starting values, at least one pixel has to be fitted beforehand by the user.

The seed pixel(s) should be selected to require the most complex model present in the dataset, however in-built goodness of fit checks ensure that only sufficiently well fitted values are allowed to propagate.

If the dataset consists of regions (in the navigation space) of highly dissimilar pixels, often called “domain structures”, at least one seed pixel should be given for each unique region.

If the starting pixels were not optimal, only part of the dataset will be fitted. In such cases it is best to allow the algorithm terminate, then provide new (better) seed pixels by hand, and restart SAMFire. It will use the new seed together with the already computed parts of the data.

Usage

After creating a model and fitting suitable seed pixels, to fit the rest of the multi-dimensional dataset using SAMFire we must create a SAMFire instance as follows:

>>> samf = m.create_samfire(workers=None, ipyparallel=False)

By default SAMFire will look for an ipyparallel cluster for the workers for around 30 seconds. If none is available, it will use multiprocessing instead. However, if you are not planning to use ipyparallel, it’s recommended specify it explicitly via the ipyparallel=False argument, to use the fall-back option of multiprocessing.

By default a new SAMFire object already has two (and currently only) strategies added to its strategist list:

>>> samf.strategies
  A |    # | Strategy
 -- | ---- | -------------------------
  x |    0 | Reduced chi squared strategy
    |    1 | Histogram global strategy

The currently active strategy is marked by an ‘x’ in the first column.

If a new datapoint (i.e. pixel) is added manually, the “database” of the currently active strategy has to be refreshed using the refresh_database() call.

The current strategy “database” can be plotted using the plot() method.

Whilst SAMFire is running, each pixel is checked by a goodness_test, which is by default red_chisq_test, checking the reduced chi-squared to be in the bounds of [0, 2].

This tolerance can (and most likely should!) be changed appropriately for the data as follows:

>>> samf.metadata.goodness_test.tolerance = 0.3 # use a sensible value

The SAMFire managed multi-dimensional fit can be started using the start() method. All keyword arguments are passed to the underlying (i.e. usual) fit() call:

>>> samf.start(fitter='mpfit', bounded=True)