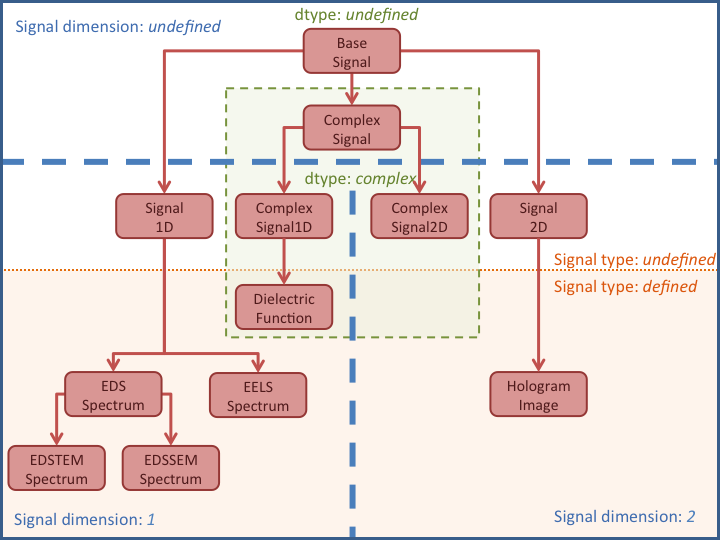
The Signal class
The Signal class and its subclasses
Warning
This subsection can be a bit confusing for beginners. Do not worry if you do not understand it all.
HyperSpy stores the data in the BaseSignal class, that is
the object that you get when e.g. you load a single file using
load(). Most of the data analysis functions are also contained in
this class or its specialized subclasses. The BaseSignal
class contains general functionality that is available to all the subclasses.
The subclasses provide functionality that is normally specific to a particular
type of data, e.g. the Signal1D class provides
common functionality to deal with one-dimensional (e.g. spectral) data and
EELSSpectrum (which is a subclass of
Signal1D) adds extra functionality to the
Signal1D class for electron energy-loss
spectroscopy data analysis.
The table below summarises all the
specialised BaseSignal subclasses currently distributed
with HyperSpy.
The signals module, which contains all available signal subclasses,
is imported in the user namespace when loading HyperSpy. In the following
example we create a Signal2D instance from a 2D numpy array:
>>> im = hs.signals.Signal2D(np.random.random((64,64)))
>>> im
<Signal2D, title: , dimensions: (|64, 64)>
The different signals store other objects in what are called attributes. For
examples, the data is stored in a numpy array in the
data attribute, the original parameters in the
original_metadata attribute, the mapped parameters
in the metadata attribute and the axes
information (including calibration) can be accessed (and modified) in the
AxesManager attribute.
Signal initialization
Many of the values in the AxesManager can be
set when making the BaseSignal object.
>>> dict0 = {'size': 10, 'name':'Axis0', 'units':'A', 'scale':0.2, 'offset':1}
>>> dict1 = {'size': 20, 'name':'Axis1', 'units':'B', 'scale':0.1, 'offset':2}
>>> s = hs.signals.BaseSignal(np.random.random((10,20)), axes=[dict0, dict1])
>>> s.axes_manager
<Axes manager, axes: (|20, 10)>
Name | size | index | offset | scale | units
================ | ====== | ====== | ======= | ======= | ======
---------------- | ------ | ------ | ------- | ------- | ------
Axis1 | 20 | | 2 | 0.1 | B
Axis0 | 10 | | 1 | 0.2 | A
This also applies to the metadata.
>>> metadata_dict = {'General':{'name':'A BaseSignal'}}
>>> metadata_dict['General']['title'] = 'A BaseSignal title'
>>> s = hs.signals.BaseSignal(np.arange(10), metadata=metadata_dict)
>>> s.metadata
├── General
│ ├── name = A BaseSignal
│ └── title = A BaseSignal title
└── Signal
└── signal_type =
Instead of using a list of axes dictionaries [dict0, dict1] during signal
initialization, you can also pass a list of axes objects: [axis0, axis1].
The navigation and signal dimensions
HyperSpy can deal with data of arbitrary dimensions. Each dimension is internally classified as either “navigation” or “signal” and the way this classification is done determines the behaviour of the signal.
The concept is probably best understood with an example: let’s imagine a three
dimensional dataset e.g. a numpy array with dimensions (10, 20, 30). This
dataset could be an spectrum image acquired by scanning over a sample in two
dimensions. As in this case the signal is one-dimensional we use a
Signal1D subclass for this data e.g.:
>>> s = hs.signals.Signal1D(np.random.random((10, 20, 30)))
>>> s
<Signal1D, title: , dimensions: (20, 10|30)>
In HyperSpy’s terminology, the signal dimension of this dataset is 30 and the navigation dimensions (20, 10). Notice the separator | between the navigation and signal dimensions.
However, the same dataset could also be interpreted as an image
stack instead. Actually it could has been acquired by capturing two
dimensional images at different wavelengths. Then it would be natural to
identify the two spatial dimensions as the signal dimensions and the wavelength
dimension as the navigation dimension. To view the data in this way we could
have used a Signal2D instead e.g.:
>>> im = hs.signals.Signal2D(np.random.random((10, 20, 30)))
>>> im
<Signal2D, title: , dimensions: (10|30, 20)>
Indeed, for data analysis purposes, one may like to operate with an image stack as if it was a set of spectra or viceversa. One can easily switch between these two alternative ways of classifying the dimensions of a three-dimensional dataset by transforming between BaseSignal subclasses.
The same dataset could be seen as a three-dimensional signal:
>>> td = hs.signals.BaseSignal(np.random.random((10, 20, 30)))
>>> td
<BaseSignal, title: , dimensions: (|30, 20, 10)>
Notice that with use BaseSignal because there is
no specialised subclass for three-dimensional data. Also note that by default
BaseSignal interprets all dimensions as signal dimensions.
We could also configure it to operate on the dataset as a three-dimensional
array of scalars by changing the default view of
BaseSignal by taking the transpose of it:
>>> scalar = td.T
>>> scalar
<BaseSignal, title: , dimensions: (30, 20, 10|)>
For more examples of manipulating signal axes in the “signal-navigation” space can be found in Transposing (changing signal spaces).
Note
Although each dimension can be arbitrarily classified as “navigation dimension” or “signal dimension”, for most common tasks there is no need to modify HyperSpy’s default choice.
Transforming between signal subclasses
The different subclasses are characterized by the signal_type metadata attribute,
the data dtype and the signal dimension. See the table and diagram below.
signal_type describes the nature of the signal. It can be any string, normally the
acronym associated with a particular signal. In certain cases HyperSpy provides
features that are only available for a particular signal type through
BaseSignal subclasses. The BaseSignal method
set_signal_type() changes the signal_type in place, which
may result in a BaseSignal subclass transformation.
Furthermore, the dtype of the signal data also affects the subclass assignment. There are e.g. specialised signal subclasses to handle complex data (see the following diagram).
Diagram showing the inheritance structure of the different subclasses
BaseSignal subclass |
signal_dimension |
signal_type |
dtype |
|---|---|---|---|
real |
|||
1 |
real |
||
1 |
EELS |
real |
|
1 |
EDS_SEM |
real |
|
|
1 |
EDS_TEM |
real |
2 |
real |
||
2 |
hologram |
real |
|
1 |
DielectricFunction |
complex |
|
complex |
|||
1 |
complex |
||
|
2 |
complex |
Changed in version 1.0: Simulation, SpectrumSimulation and ImageSimulation
classes removed.
New in version 1.5: External packages can register extra BaseSignal
subclasses.
Note that, if you have packages that extend HyperSpy installed in your system, there may
be more specialised signals available to you. To print all available specialised
BaseSignal subclasses installed in your system call the
print_known_signal_types()
function as in the following example:
>>> hs.print_known_signal_types()
+--------------------+---------------------+--------------------+----------+
| signal_type | aliases | class name | package |
+--------------------+---------------------+--------------------+----------+
| DielectricFunction | dielectric function | DielectricFunction | hyperspy |
| EDS_SEM | | EDSSEMSpectrum | hyperspy |
| EDS_TEM | | EDSTEMSpectrum | hyperspy |
| EELS | TEM EELS | EELSSpectrum | hyperspy |
| hologram | | HologramImage | hyperspy |
| MySignal | | MySignal | hspy_ext |
+--------------------+---------------------+--------------------+----------+
Warning
From version 2.0 HyperSpy will no longer ship
BaseSignal subclasses that are specific to a
particular type of data (i.e. with non-empty signal_type). All those
signals currently distributed with HyperSpy will be moved to new
packages.
The following example shows how to transform between different subclasses.
>>> s = hs.signals.Signal1D(np.random.random((10,20,100))) >>> s <Signal1D, title: , dimensions: (20, 10|100)> >>> s.metadata ├── signal_type = └── title = >>> im = s.to_signal2D() >>> im <Signal2D, title: , dimensions: (100|20, 10)> >>> im.metadata ├── signal_type = └── title = >>> s.set_signal_type("EELS") >>> s <EELSSpectrum, title: , dimensions: (20, 10|100)> >>> s.change_dtype("complex") >>> s <ComplexSignal1D, title: , dimensions: (20, 10|100)>
Ragged array
A ragged array (also called jagged array) is an array created with sequences-of-sequences, where the nested sequences don’t have the same length. For example, a numpy ragged array can be created as follow:
>>> arr = np.array([[1, 2, 3], [1]], dtype=object) >>> arr array([list([1, 2, 3]), list([1])], dtype=object)
Note that the array shape is (2, ):
>>> arr.shape (2, )
Numpy ragged array must have python object type to allow the variable length of
the nested sequences - here [1, 2, 3] and [1]. As explained in
NEP-34,
dtype=object needs to be specified when creating the array to avoid ambiguity
about the shape of the array.
HyperSpy supports the use of ragged array with the following conditions:
The signal must be explicitly defined as being
ragged, either when creating the signal or by changing the ragged attribute of the signalThe signal dimension is the variable length dimension of the array
The
isigsyntax is not supportedSignal with ragged array can’t be transposed
Signal with ragged array can’t be plotted
To create a hyperspy signal of a numpy ragged array:
>>> s = hs.signals.BaseSignal(arr, ragged=True) >>> s <BaseSignal, title: , dimensions: (2|ragged)> >>> s.ragged True >>> s.axes_manager <Axes manager, axes: (2|ragged)> Name | size | index | offset | scale | units ================ | ====== | ====== | ======= | ======= | ====== <undefined> | 2 | 0 | 0 | 1 | <undefined> ---------------- | ------ | ------ | ------- | ------- | ------ Ragged axis | Variable length
Note
When possible, numpy will cast sequences-of-sequences to “non-ragged” array:
>>> arr = np.array([np.array([1, 2]), np.array([1, 2])], dtype=object) >>> arr array([[1, 2], [1, 2]], dtype=object)
Unlike in the previous example, here the array is not ragged, because the length of the nested sequences are equal (2) and numpy will create an array of shape (2, 2) instead of (2, ) as in the previous example of ragged array
>>> arr.shape (2, 2)
In addition to the use of the keyword ragged when creating an hyperspy
signal, the ragged attribute can also be set to specify whether the signal
contains a ragged array or not.
In the following example, an hyperspy signal is created without specifying that
the array is ragged. In this case, the signal dimension is 2, which can be
misleading, because each item contains a list of numbers. To provide a unambiguous
representation of the fact that the signal contains a ragged array, the
ragged attribute can be set to True. By doing so, the signal space will
be described as “ragged” and the navigation shape will become the same as the
shape of the ragged array:
>>> arr = np.array([[1, 2, 3], [1]], dtype=object) >>> s = hs.signals.BaseSignal(arr) >>> s <BaseSignal, title: , dimensions: (|2)> >>> s.ragged = True >>> s <BaseSignal, title: , dimensions: (2|ragged)>
Binned and unbinned signals
Signals that are a histogram of a probability density function (pdf) should
have the is_binned attribute of the signal axis set to True. The reason
is that some methods operate differently on signals that are binned. An
example of binned signals are EDS spectra, where the multichannel analyzer
integrates the signal counts in every channel (=bin).
Note that for 2D signals each signal axis has an is_binned
attribute that can be set independently. For example, for the first signal
axis: signal.axes_manager.signal_axes[0].is_binned.
The default value of the is_binned attribute is shown in the
following table:
BaseSignal subclass |
binned |
|---|---|
False |
|
False |
|
True |
|
True |
|
True |
|
False |
|
False |
|
False |
|
False |
To change the default value:
>>> s.axes_manager[-1].is_binned = True
Changed in version 1.7: The binned attribute from the metadata has been
replaced by the axis attributes is_binned.
Integration of binned signals
For binned axes, the detector already provides the per-channel integration of
the signal. Therefore, in this case, integrate1D()
performs a simple summation along the given axis. In contrast, for unbinned
axes, integrate1D() calls the
integrate_simpson() method.
Generic tools
Below we briefly introduce some of the most commonly used tools (methods). For
more details about a particular method click on its name. For a detailed list
of all the methods available see the BaseSignal documentation.
The methods of this section are available to all the signals. In other chapters methods that are only available in specialized subclasses.
Mathematical operations
A number of mathematical operations are available
in BaseSignal. Most of them are just wrapped numpy
functions.
The methods that perform mathematical operation over one or more axis at a time are:
Note that by default all this methods perform the operation over all navigation axes.
Example:
>>> s = hs.signals.BaseSignal(np.random.random((2,4,6)))
>>> s.axes_manager[0].name = 'E'
>>> s
<BaseSignal, title: , dimensions: (|6, 4, 2)>
>>> # by default perform operation over all navigation axes
>>> s.sum()
<BaseSignal, title: , dimensions: (|6, 4, 2)>
>>> # can also pass axes individually
>>> s.sum('E')
<Signal2D, title: , dimensions: (|4, 2)>
>>> # or a tuple of axes to operate on, with duplicates, by index or directly
>>> ans = s.sum((-1, s.axes_manager[1], 'E', 0))
>>> ans
<BaseSignal, title: , dimensions: (|1)>
>>> ans.axes_manager[0]
<Scalar axis, size: 1>
The following methods operate only on one axis at a time:
All numpy ufunc can operate on BaseSignal
instances, for example:
>>> s = hs.signals.Signal1D([0, 1])
>>> s.metadata.General.title = "A"
>>> s
<Signal1D, title: A, dimensions: (|2)>
>>> np.exp(s)
<Signal1D, title: exp(A), dimensions: (|2)>
>>> np.exp(s).data
array([ 1. , 2.71828183])
>>> np.power(s, 2)
<Signal1D, title: power(A, 2), dimensions: (|2)>
>>> np.add(s, s)
<Signal1D, title: add(A, A), dimensions: (|2)>
>>> np.add(hs.signals.Signal1D([0, 1]), hs.signals.Signal1D([0, 1]))
<Signal1D, title: add(Untitled Signal 1, Untitled Signal 2), dimensions: (|2)>
Notice that the title is automatically updated. When the signal has no title a new title is automatically generated:
>>> np.add(hs.signals.Signal1D([0, 1]), hs.signals.Signal1D([0, 1]))
<Signal1D, title: add(Untitled Signal 1, Untitled Signal 2), dimensions: (|2)>
Functions (other than unfucs) that operate on numpy arrays can also operate
on BaseSignal instances, however they return a numpy
array instead of a BaseSignal instance e.g.:
>>> np.angle(s)
array([ 0., 0.])
Note
For numerical differentiation and integration, use the proper
methods derivative() and
integrate1D(). In certain cases, particularly
when operating on a non-uniform axis, the approximations using the
diff() and sum()
methods will lead to erroneous results.
Indexing
Indexing a BaseSignal provides a powerful, convenient and
Pythonic way to access and modify its data. In HyperSpy indexing is achieved
using isig and inav, which allow the navigation and signal dimensions
to be indexed independently. The idea is essentially to specify a subset of the
data based on its position in the array and it is therefore essential to know
the convention adopted for specifying that position, which is described here.
Those new to Python may find indexing a somewhat esoteric concept but once mastered it is one of the most powerful features of Python based code and greatly simplifies many common tasks. HyperSpy’s Signal indexing is similar to numpy array indexing and those new to Python are encouraged to read the associated numpy documentation on the subject.
Key features of indexing in HyperSpy are as follows (note that some of these features differ from numpy):
HyperSpy indexing does:
Allow independent indexing of signal and navigation dimensions
Support indexing with decimal numbers.
Support indexing with units.
Support indexing with relative coordinates i.e. ‘rel0.5’
Use the image order for indexing i.e. [x, y, z,…] (HyperSpy) vs […,z,y,x] (numpy)
HyperSpy indexing does not:
Support indexing using arrays.
Allow the addition of new axes using the newaxis object.
The examples below illustrate a range of common indexing tasks.
First consider indexing a single spectrum, which has only one signal dimension
(and no navigation dimensions) so we use isig:
>>> s = hs.signals.Signal1D(np.arange(10))
>>> s
<Signal1D, title: , dimensions: (|10)>
>>> s.data
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> s.isig[0]
<Signal1D, title: , dimensions: (|1)>
>>> s.isig[0].data
array([0])
>>> s.isig[9].data
array([9])
>>> s.isig[-1].data
array([9])
>>> s.isig[:5]
<Signal1D, title: , dimensions: (|5)>
>>> s.isig[:5].data
array([0, 1, 2, 3, 4])
>>> s.isig[5::-1]
<Signal1D, title: , dimensions: (|6)>
>>> s.isig[5::-1]
<Signal1D, title: , dimensions: (|6)>
>>> s.isig[5::2]
<Signal1D, title: , dimensions: (|3)>
>>> s.isig[5::2].data
array([5, 7, 9])
Unlike numpy, HyperSpy supports indexing using decimal numbers or strings (containing a decimal number and units), in which case HyperSpy indexes using the axis scales instead of the indices. Additionally, one can index using relative coordinates, for example ‘rel0.5’ to index the middle of the axis.
>>> s = hs.signals.Signal1D(np.arange(10))
>>> s
<Signal1D, title: , dimensions: (|10)>
>>> s.data
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> s.axes_manager[0].scale = 0.5
>>> s.axes_manager[0].axis
array([ 0. , 0.5, 1. , 1.5, 2. , 2.5, 3. , 3.5, 4. , 4.5])
>>> s.isig[0.5:4.].data
array([1, 2, 3, 4, 5, 6, 7])
>>> s.isig[0.5:4].data
array([1, 2, 3])
>>> s.isig[0.5:4:2].data
array([1, 3])
>>> s.axes_manager[0].units = 'µm'
>>> s.isig[:'2000 nm'].data
array([0, 1, 2, 3])
>>> s.isig[:'rel0.5'].data
array([0, 1, 2, 3])
Importantly the original BaseSignal and its “indexed self”
share their data and, therefore, modifying the value of the data in one
modifies the same value in the other. Note also that in the example below
s.data is used to access the data as a numpy array directly and this array is
then indexed using numpy indexing.
>>> s = hs.signals.Signal1D(np.arange(10))
>>> s
<Signal1D, title: , dimensions: (10,)>
>>> s.data
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> si = s.isig[::2]
>>> si.data
array([0, 2, 4, 6, 8])
>>> si.data[:] = 10
>>> si.data
array([10, 10, 10, 10, 10])
>>> s.data
array([10, 1, 10, 3, 10, 5, 10, 7, 10, 9])
>>> s.data[:] = 0
>>> si.data
array([0, 0, 0, 0, 0])
Of course it is also possible to use the same syntax to index multidimensional
data treating navigation axes using inav and signal axes using isig.
>>> s = hs.signals.Signal1D(np.arange(2*3*4).reshape((2,3,4)))
>>> s
<Signal1D, title: , dimensions: (3, 2|4)>
>>> s.data
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
>>> s.axes_manager[0].name = 'x'
>>> s.axes_manager[1].name = 'y'
>>> s.axes_manager[2].name = 't'
>>> s.axes_manager.signal_axes
(<t axis, size: 4>,)
>>> s.axes_manager.navigation_axes
(<x axis, size: 3, index: 0>, <y axis, size: 2, index: 0>)
>>> s.inav[0,0].data
array([0, 1, 2, 3])
>>> s.inav[0,0].axes_manager
<Axes manager, axes: (|4)>
Name | size | index | offset | scale | units
================ | ====== | ====== | ======= | ======= | ======
---------------- | ------ | ------ | ------- | ------- | ------
t | 4 | | 0 | 1 | <undefined>
>>> s.inav[0,0].isig[::-1].data
array([3, 2, 1, 0])
>>> s.isig[0]
<BaseSignal, title: , dimensions: (3, 2)>
>>> s.isig[0].axes_manager
<Axes manager, axes: (3, 2|)>
Name | size | index | offset | scale | units
================ | ====== | ====== | ======= | ======= | ======
x | 3 | 0 | 0 | 1 | <undefined>
y | 2 | 0 | 0 | 1 | <undefined>
---------------- | ------ | ------ | ------- | ------- | ------
>>> s.isig[0].data
array([[ 0, 4, 8],
[12, 16, 20]])
Independent indexation of the signal and navigation dimensions is demonstrated further in the following:
>>> s = hs.signals.Signal1D(np.arange(2*3*4).reshape((2,3,4)))
>>> s
<Signal1D, title: , dimensions: (3, 2|4)>
>>> s.data
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
>>> s.axes_manager[0].name = 'x'
>>> s.axes_manager[1].name = 'y'
>>> s.axes_manager[2].name = 't'
>>> s.axes_manager.signal_axes
(<t axis, size: 4>,)
>>> s.axes_manager.navigation_axes
(<x axis, size: 3, index: 0>, <y axis, size: 2, index: 0>)
>>> s.inav[0,0].data
array([0, 1, 2, 3])
>>> s.inav[0,0].axes_manager
<Axes manager, axes: (|4)>
Name | size | index | offset | scale | units
================ | ====== | ====== | ======= | ======= | ======
---------------- | ------ | ------ | ------- | ------- | ------
t | 4 | | 0 | 1 | <undefined>
>>> s.isig[0]
<BaseSignal, title: , dimensions: (2, 3)>
>>> s.isig[0].axes_manager
<Axes manager, axes: (3, 2|)>
Name | size | index | offset | scale | units
================ | ====== | ====== | ======= | ======= | ======
x | 3 | 0 | 0 | 1 | <undefined>
y | 2 | 0 | 0 | 1 | <undefined>
---------------- | ------ | ------ | ------- | ------- | ------
>>> s.isig[0].data
array([[ 0, 4, 8],
[12, 16, 20]])
The same syntax can be used to set the data values in signal and navigation dimensions respectively:
>>> s = hs.signals.Signal1D(np.arange(2*3*4).reshape((2,3,4)))
>>> s
<Signal1D, title: , dimensions: (3, 2|4)>
>>> s.data
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
>>> s.inav[0,0].data
array([0, 1, 2, 3])
>>> s.inav[0,0] = 1
>>> s.inav[0,0].data
array([1, 1, 1, 1])
>>> s.inav[0,0] = s.inav[1,1]
>>> s.inav[0,0].data
array([16, 17, 18, 19])
Signal operations
BaseSignal supports all the Python binary arithmetic
operations (+, -, *, //, %, divmod(), pow(), **, <<, >>, &, ^, |),
augmented binary assignments (+=, -=, *=, /=, //=, %=, **=, <<=, >>=, &=,
^=, |=), unary operations (-, +, abs() and ~) and rich comparisons operations
(<, <=, ==, x!=y, <>, >, >=).
These operations are performed element-wise. When the dimensions of the signals are not equal numpy broadcasting rules apply independently for the navigation and signal axes.
Warning
Hyperspy does not check if the calibration of the signals matches.
In the following example s2 has only one navigation axis while s has two. However, because the size of their first navigation axis is the same, their dimensions are compatible and s2 is broadcasted to match s’s dimensions.
>>> s = hs.signals.Signal2D(np.ones((3,2,5,4)))
>>> s2 = hs.signals.Signal2D(np.ones((2,5,4)))
>>> s
<Signal2D, title: , dimensions: (2, 3|4, 5)>
>>> s2
<Signal2D, title: , dimensions: (2|4, 5)>
>>> s + s2
<Signal2D, title: , dimensions: (2, 3|4, 5)>
In the following example the dimensions are not compatible and an exception is raised.
>>> s = hs.signals.Signal2D(np.ones((3,2,5,4)))
>>> s2 = hs.signals.Signal2D(np.ones((3,5,4)))
>>> s
<Signal2D, title: , dimensions: (2, 3|4, 5)>
>>> s2
<Signal2D, title: , dimensions: (3|4, 5)>
>>> s + s2
Traceback (most recent call last):
File "<ipython-input-55-044bb11a0bd9>", line 1, in <module>
s + s2
File "<string>", line 2, in __add__
File "/home/fjd29/Python/hyperspy/hyperspy/signal.py", line 2686, in _binary_operator_ruler
raise ValueError(exception_message)
ValueError: Invalid dimensions for this operation
Broadcasting operates exactly in the same way for the signal axes:
>>> s = hs.signals.Signal2D(np.ones((3,2,5,4)))
>>> s2 = hs.signals.Signal1D(np.ones((3, 2, 4)))
>>> s
<Signal2D, title: , dimensions: (2, 3|4, 5)>
>>> s2
<Signal1D, title: , dimensions: (2, 3|4)>
>>> s + s2
<Signal2D, title: , dimensions: (2, 3|4, 5)>
In-place operators also support broadcasting, but only when broadcasting would not change the left most signal dimensions:
>>> s += s2
>>> s
<Signal2D, title: , dimensions: (2, 3|4, 5)>
>>> s2 += s
Traceback (most recent call last):
File "<ipython-input-64-fdb9d3a69771>", line 1, in <module>
s2 += s
File "<string>", line 2, in __iadd__
File "/home/fjd29/Python/hyperspy/hyperspy/signal.py", line 2737, in _binary_operator_ruler
self.data = getattr(sdata, op_name)(odata)
ValueError: non-broadcastable output operand with shape (3,2,1,4) doesn\'t match the broadcast shape (3,2,5,4)
Iterating over the navigation axes
BaseSignal instances are iterables over the navigation axes. For example, the following code creates a stack of 10 images and saves them in separate “png” files by iterating over the signal instance:
>>> image_stack = hs.signals.Signal2D(np.random.random((2, 5, 64,64)))
>>> for single_image in image_stack:
... single_image.save("image %s.png" % str(image_stack.axes_manager.indices))
The "image (0, 0).png" file was created.
The "image (1, 0).png" file was created.
The "image (2, 0).png" file was created.
The "image (3, 0).png" file was created.
The "image (4, 0).png" file was created.
The "image (0, 1).png" file was created.
The "image (1, 1).png" file was created.
The "image (2, 1).png" file was created.
The "image (3, 1).png" file was created.
The "image (4, 1).png" file was created.
The data of the signal instance that is returned at each iteration is a view of
the original data, a property that we can use to perform operations on the
data. For example, the following code rotates the image at each coordinate by
a given angle and uses the stack() function in combination
with list comprehensions
to make a horizontal “collage” of the image stack:
>>> import scipy.ndimage
>>> image_stack = hs.signals.Signal2D(np.array([scipy.misc.ascent()]*5))
>>> image_stack.axes_manager[1].name = "x"
>>> image_stack.axes_manager[2].name = "y"
>>> for image, angle in zip(image_stack, (0, 45, 90, 135, 180)):
... image.data[:] = scipy.ndimage.rotate(image.data, angle=angle,
... reshape=False)
>>> # clip data to integer range:
>>> image_stack.data = np.clip(image_stack.data, 0, 255)
>>> collage = hs.stack([image for image in image_stack], axis=0)
>>> collage.plot(scalebar=False)
Rotation of images by iteration.
Iterating external functions with the map method
Performing an operation on the data at each coordinate, as in the previous example,
using an external function can be more easily accomplished using the
map() method:
>>> import scipy.ndimage
>>> image_stack = hs.signals.Signal2D(np.array([scipy.misc.ascent()]*4))
>>> image_stack.axes_manager[1].name = "x"
>>> image_stack.axes_manager[2].name = "y"
>>> image_stack.map(scipy.ndimage.rotate,
... angle=45,
... reshape=False)
>>> # clip data to integer range
>>> image_stack.data = np.clip(image_stack.data, 0, 255)
>>> collage = hs.stack([image for image in image_stack], axis=0)
>>> collage.plot()
The map() method can also take variable
arguments as in the following example.
>>> import scipy.ndimage
>>> image_stack = hs.signals.Signal2D(np.array([scipy.misc.ascent()]*4))
>>> image_stack.axes_manager[1].name = "x"
>>> image_stack.axes_manager[2].name = "y"
>>> angles = hs.signals.BaseSignal(np.array([0, 45, 90, 135]))
>>> image_stack.map(scipy.ndimage.rotate,
... angle=angles.T,
... reshape=False)
Rotation of images using map() with different
arguments for each image in the stack.
New in version 1.2.0: inplace keyword and non-preserved output shapes
If all function calls do not return identically-shaped results, only navigation information is preserved, and the final result is an array where each element corresponds to the result of the function (or arbitrary object type). These are ragged arrays and has the dtype object. As such, most HyperSpy functions cannot operate on such signals, and the data should be accessed directly.
The inplace keyword (by default True) of the
map() method allows either overwriting the current
data (default, True) or storing it to a new signal (False).
>>> import scipy.ndimage
>>> image_stack = hs.signals.Signal2D(np.array([scipy.misc.ascent()]*4))
>>> angles = hs.signals.BaseSignal(np.array([0, 45, 90, 135]))
>>> result = image_stack.map(scipy.ndimage.rotate,
... angle=angles.T,
... inplace=False,
... ragged=True,
... reshape=True)
100%|████████████████████████████████████████████| 4/4 [00:00<00:00, 18.42it/s]
>>> result
<BaseSignal, title: , dimensions: (4|)>
>>> result.data.dtype
dtype('O')
>>> for d in result.data.flat:
... print(d.shape)
(512, 512)
(724, 724)
(512, 512)
(724, 724)
The execution can be sped up by passing parallel keyword to the
map() method:
>>> import time
>>> def slow_func(data):
... time.sleep(1.)
... return data + 1
>>> s = hs.signals.Signal1D(np.arange(40).reshape((20, 2)))
>>> s
<Signal1D, title: , dimensions: (20|2)>
>>> s.map(slow_func, parallel=False)
100%|██████████████████████████████████████| 20/20 [00:20<00:00, 1.00s/it]
>>> # some operations will be done in parallel:
>>> s.map(slow_func, parallel=True)
100%|██████████████████████████████████████| 20/20 [00:02<00:00, 6.73it/s]
Note
HyperSpy implements thread-based parallelism for the map()
method. You can control the number of threads that are created by passing an integer value
to the max_workers keyword argument. By default, it will use min(32, os.cpu_count()).
New in version 1.4: Iterating over signal using a parameter with no navigation dimension.
In this case, the parameter is cyclically iterated over the navigation dimension of the input signal. In the example below, signal s is multiplied by a cosine parameter d, which is repeated over the navigation dimension of s.
>>> s = hs.signals.Signal1D(np.random.rand(10, 512))
>>> d = hs.signals.Signal1D(np.cos(np.linspace(0., 2*np.pi, 512)))
>>> s.map(lambda A, B: A * B, B=d)
100%|██████████| 10/10 [00:00<00:00, 2573.19it/s]
New in version 1.7: Get result as lazy signal
Especially when working with very large datasets, it can be useful to not do the computation immediately. For example if it would make you run out of memory. In that case, the lazy_output parameter can be used.
>>> from scipy.ndimage import gaussian_filter
>>> s = hs.signals.Signal2D(np.random.random((4, 4, 128, 128)))
>>> s_out = s.map(gaussian_filter, sigma=5, inplace=False, lazy_output=True)
<LazySignal2D, title: , dimensions: (4, 4|128, 128)>
s_out can then be saved to a hard drive, to avoid it being loaded into memory. Alternatively, it can be computed and loaded into memory using s_out.compute()
>>> s_out.save("gaussian_filter_file.hspy")
Another advantage of using lazy_output=True is the ability to “chain” operations, by running map on the output from a previous map operation. For example, first running a Gaussian filter, followed by peak finding. This can improve the computation time, and reduce the memory need.
>>> s_out = s.map(scipy.ndimage.gaussian_filter, sigma=5, inplace=False, lazy_output=True)
>>> from skimage.feature import blob_dog
>>> s_out1 = s_out.map(blob_dog, threshold=0.05, inplace=False, ragged=True, lazy_output=False)
>>> s_out1
<BaseSignal, title: , dimensions: (4, 4|ragged)>
This is especially relevant for very large datasets, where memory use can be a limiting factor.
Cropping
Cropping can be performed in a very compact and powerful way using
Indexing . In addition it can be performed using the following
method or GUIs if cropping signal1D or signal2D. There is also a general crop()
method that operates in place.
Rebinning
New in version 1.3: rebin() generalized to remove the constrain
of the new_shape needing to be a divisor of data.shape.
The rebin() methods supports rebinning the data to
arbitrary new shapes as long as the number of dimensions stays the same.
However, internally, it uses two different algorithms to perform the task. Only
when the new shape dimensions are divisors of the old shape’s, the operation
supports lazy-evaluation and is usually faster.
Otherwise, the operation requires linear interpolation.
For example, the following two equivalent rebinning operations can be performed lazily:
>>> s = hs.datasets.example_signals.EDS_SEM_Spectrum().as_lazy()
>>> print(s)
<LazyEDSSEMSpectrum, title: EDS SEM Spectrum, dimensions: (|1024)>
>>> print(s.rebin(scale=[2]))
<LazyEDSSEMSpectrum, title: EDS SEM Spectrum, dimensions: (|512)>
>>> s = hs.datasets.example_signals.EDS_SEM_Spectrum().as_lazy()
>>> print(s.rebin(new_shape=[512]))
<LazyEDSSEMSpectrum, title: EDS SEM Spectrum, dimensions: (|512)>
On the other hand, the following rebinning operation requires interpolation and cannot be performed lazily:
>>> spectrum = hs.signals.EDSTEMSpectrum(np.ones([4, 4, 10]))
>>> spectrum.data[1, 2, 9] = 5
>>> print(spectrum)
<EDSTEMSpectrum, title: , dimensions: (4, 4|10)>
>>> print ('Sum = ', spectrum.data.sum())
Sum = 164.0
>>> scale = [0.5, 0.5, 5]
>>> test = spectrum.rebin(scale=scale)
>>> test2 = spectrum.rebin(new_shape=(8, 8, 2)) # Equivalent to the above
>>> print(test)
<EDSTEMSpectrum, title: , dimensions: (8, 8|2)>
>>> print(test2)
<EDSTEMSpectrum, title: , dimensions: (8, 8|2)>
>>> print('Sum =', test.data.sum())
Sum = 164.0
>>> print('Sum =', test2.data.sum())
Sum = 164.0
>>> spectrum.as_lazy().rebin(scale=scale)
Traceback (most recent call last):
File "<ipython-input-26-49bca19ebf34>", line 1, in <module>
spectrum.as_lazy().rebin(scale=scale)
File "/home/fjd29/Python/hyperspy3/hyperspy/_signals/eds.py", line 184, in rebin
m = super().rebin(new_shape=new_shape, scale=scale, crop=crop, out=out)
File "/home/fjd29/Python/hyperspy3/hyperspy/_signals/lazy.py", line 246, in rebin
"Lazy rebin requires scale to be integer and divisor of the "
NotImplementedError: Lazy rebin requires scale to be integer and divisor of the original signal shape
The dtype argument can be used to specify the dtype of the returned
signal:
>>> s = hs.signals.Signal1D(np.ones((2, 5, 10), dtype=np.uint8)
>>> print(s)
<Signal1D, title: , dimensions: (5, 2|10)>
>>> print(s.data.dtype)
uint8
# Use dtype=np.unit16 to specify a dtype
>>> s2 = s.rebin(scale=(5, 2, 1), dtype=np.uint16)
>>> print(s2.data.dtype)
uint16
# Use dtype="same" to keep the same dtype
>>> s3 = s.rebin(scale=(5, 2, 1), dtype="same")
>>> print(s3.data.dtype)
uint8
# By default `dtype=None`, the dtype is determined by the behaviour of
# numpy.sum, in this case, unsigned integer of the same precision as the
# platform interger
>>> s4 = s.rebin(scale=(5, 2, 1))
>>> print(s4.data.dtype)
uint64
Squeezing
The squeeze() method removes any zero-dimensional
axes, i.e. axes of size=1, and the attributed data dimensions from a signal.
The method returns a reduced copy of the signal and does not operate in place.
>>> s = hs.signals.Signal2D(np.random.random((2,1,1,6,8,8)))
<Signal2D, title: , dimensions: (6, 1, 1, 2|8, 8)>
>>> s = s.squeeze()
>>> s
<Signal2D, title: , dimensions: (6, 2|8, 8)>
Squeezing can be particularly useful after a rebinning operation that leaves
one dimension with shape=1:
>>> s = hs.signals.Signal2D(np.random.random((5,5,5,10,10)))
>>> s.rebin(new_shape=(5,1,5,5,5))
<Signal2D, title: , dimensions: (5, 1, 5|5, 5)>
>>> s.rebin(new_shape=(5,1,5,5,5)).squeeze()
<Signal2D, title: , dimensions: (5, 5|5, 5)>
Folding and unfolding
When dealing with multidimensional datasets it is sometimes useful to transform the data into a two dimensional dataset. This can be accomplished using the following two methods:
It is also possible to unfold only the navigation or only the signal space:
Splitting and stacking
Several objects can be stacked together over an existing axis or over a
new axis using the stack() function, if they share axis
with same dimension.
>>> image = hs.signals.Signal2D(scipy.misc.ascent())
>>> image = hs.stack([hs.stack([image]*3,axis=0)]*3,axis=1)
>>> image.plot()
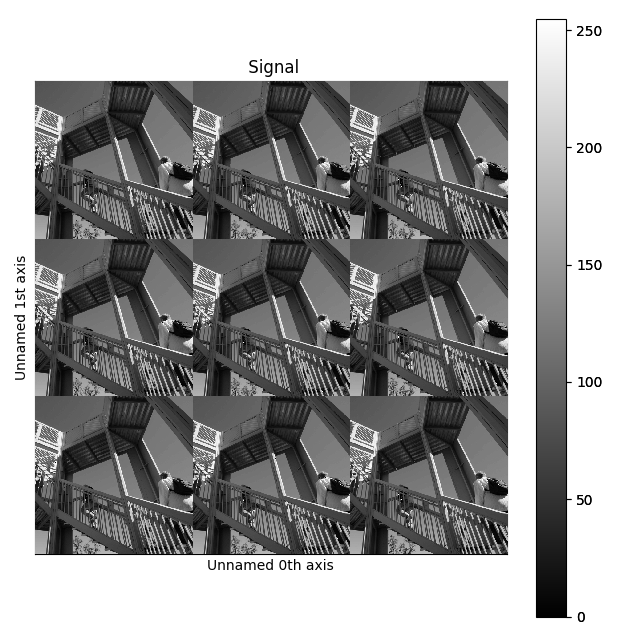
Stacking example.
Note
When stacking signals with large amount of
original_metadata, these metadata will be
stacked and this can lead to very large amount of metadata which can in
turn slow down processing. The stack_original_metadata argument can be
used to disable stacking original_metadata.
An object can be split into several objects
with the split() method. This function can be used
to reverse the stack() function:
>>> image = image.split()[0].split()[0]
>>> image.plot()
Splitting example.
Fast Fourier Transform (FFT)
The fast Fourier transform
of a signal can be computed using the fft() method. By default,
the FFT is calculated with the origin at (0, 0), which will be displayed at the
bottom left and not in the centre of the FFT. Conveniently, the shift argument of the
the fft() method can be used to center the output of the FFT.
In the following example, the FFT of a hologram is computed using shift=True and its
output signal is displayed, which shows that the FFT results in a complex signal with a
real and an imaginary parts:
>>> im = hs.datasets.example_signals.reference_hologram()
>>> fft_shifted = im.fft(shift=True)
>>> fft_shifted.plot()
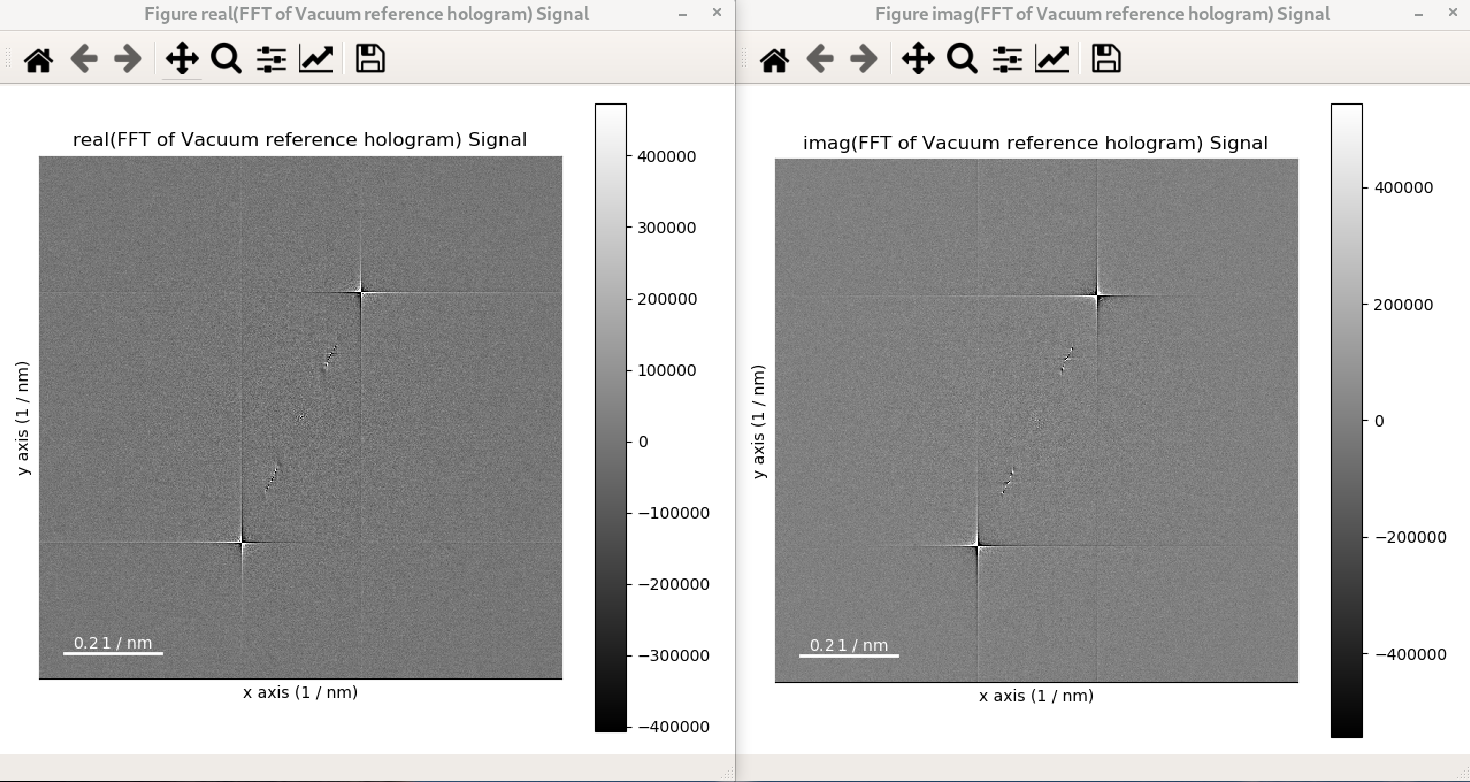
The strong features in the real and imaginary parts correspond to the lattice fringes of the hologram.
For visual inspection of the FFT it is convenient to display its power spectrum
(i.e. the square of the absolute value of the FFT) rather than FFT itself as it is done
in the example above by using the power_spectum argument:
>>> im = hs.datasets.example_signals.reference_hologram()
>>> fft = im.fft(True)
>>> fft.plot(True)
Where power_spectum is set to True since it is the first argument of the
plot() method for complex signal.
When power_spectrum=True, the plot will be displayed on a log scale by default.
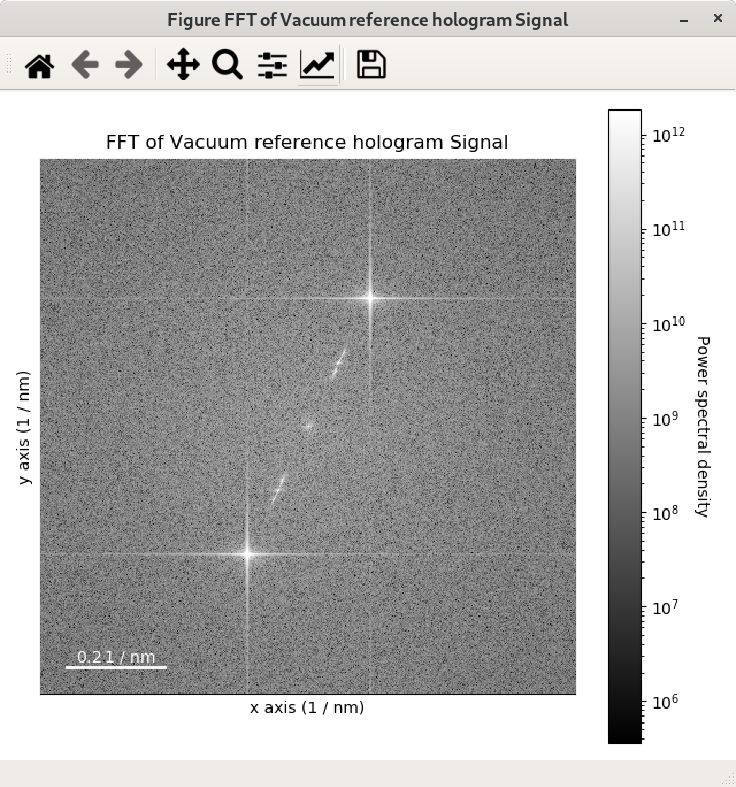
The visualisation can be further improved by setting the minimum value to display to the 30-th
percentile; this can be done by using vmin="30th" in the plot function:
>>> im = hs.datasets.example_signals.reference_hologram()
>>> fft = im.fft(True)
>>> fft.plot(True, vmin="30th")
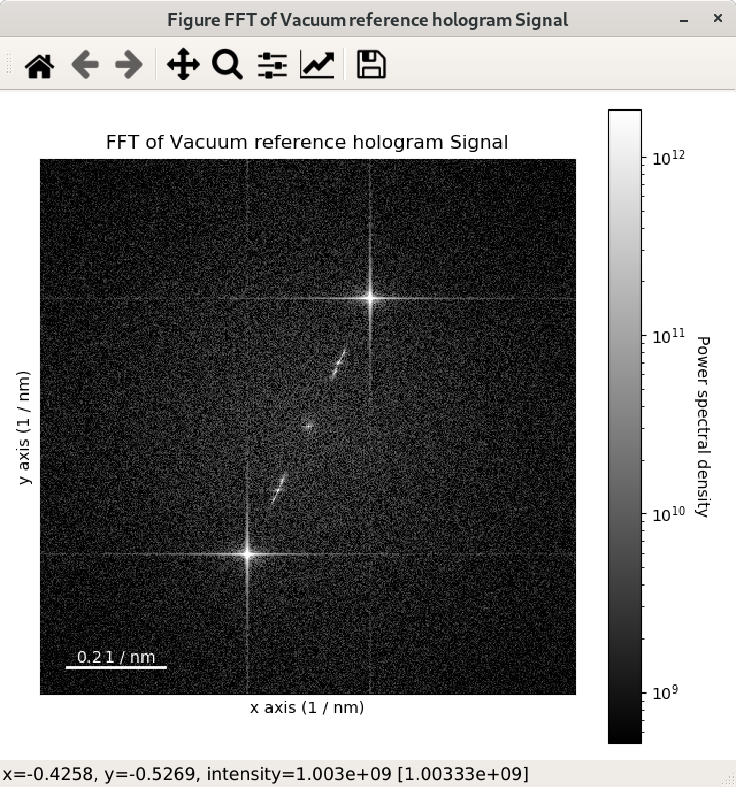
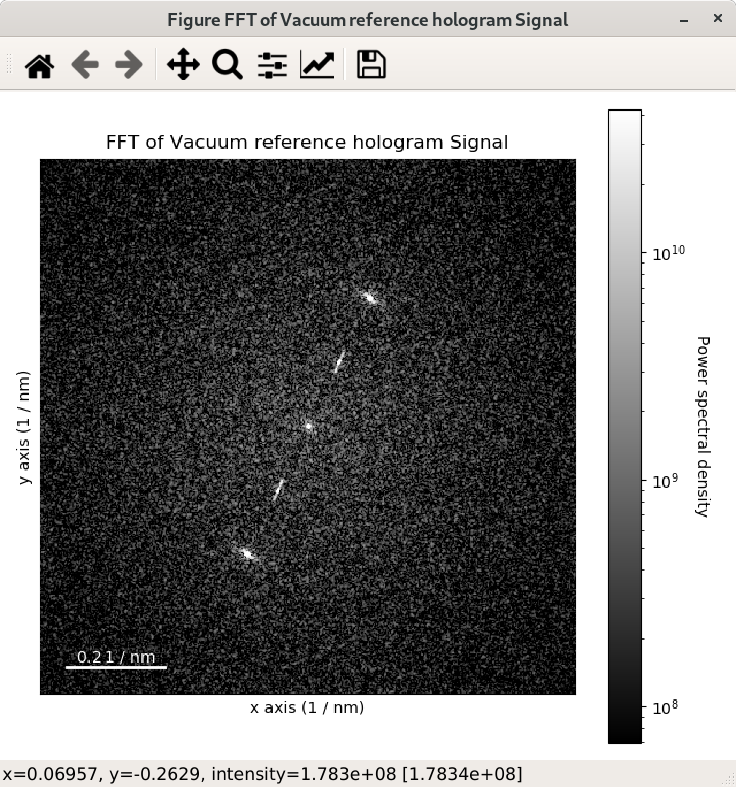
The streaks visible in the FFT come from the edge of the image and can be removed by
applying an apodization function to the original
signal before the computation of the FFT. This can be done using the apodization argument of
the fft() method and it is usually used for visualising FFT patterns
rather than for quantitative analyses. By default, the so-called hann windows is
used but different type of windows such as the hamming and tukey windows.
>>> im = hs.datasets.example_signals.reference_hologram()
>>> fft = im.fft(shift=True)
>>> fft_apodized = im.fft(shift=True, apodization=True)
>>> fft_apodized.plot(True, vmin="30th")
Inverse Fast Fourier Transform (iFFT)
Inverse fast Fourier transform can be calculated from a complex signal by using the
ifft() method. Similarly to the fft() method,
the shift argument can be provided to shift the origin of the iFFT when necessary:
>>> im_ifft = im.fft(shift=True).ifft(shift=True)
Changing the data type
Even if the original data is recorded with a limited dynamic range, it is often
desirable to perform the analysis operations with a higher precision.
Conversely, if space is limited, storing in a shorter data type can decrease
the file size. The change_dtype() changes the data
type in place, e.g.:
>>> s = hs.load('EELS Signal1D Signal2D (high-loss).dm3')
Title: EELS Signal1D Signal2D (high-loss).dm3
Signal type: EELS
Data dimensions: (21, 42, 2048)
Data representation: spectrum
Data type: float32
>>> s.change_dtype('float64')
>>> print(s)
Title: EELS Signal1D Signal2D (high-loss).dm3
Signal type: EELS
Data dimensions: (21, 42, 2048)
Data representation: spectrum
Data type: float64
In addition to all standard numpy dtypes, HyperSpy supports four extra dtypes
for RGB images for visualization purposes only: rgb8, rgba8,
rgb16 and rgba16. This includes of course multi-dimensional RGB images.
The requirements for changing from and to any rgbx dtype are more strict
than for most other dtype conversions. To change to a rgbx dtype the
signal_dimension must be 1 and its size 3 (4) 3(4) for rgb (or
rgba) dtypes and the dtype must be uint8 (uint16) for
rgbx8 (rgbx16). After conversion the signal_dimension becomes 2.
Most operations on signals with RGB dtypes will fail. For processing simply
change their dtype to uint8 (uint16).The dtype of images of
dtype rgbx8 (rgbx16) can only be changed to uint8 (uint16) and
the signal_dimension becomes 1.
In the following example we create a 1D signal with signal size 3 and with
dtype uint16 and change its dtype to rgb16 for plotting.
>>> rgb_test = np.zeros((1024, 1024, 3))
>>> ly, lx = rgb_test.shape[:2]
>>> offset_factor = 0.16
>>> size_factor = 3
>>> Y, X = np.ogrid[0:lx, 0:ly]
>>> rgb_test[:,:,0] = (X - lx / 2 - lx*offset_factor) ** 2 + \
... (Y - ly / 2 - ly*offset_factor) ** 2 < \
... lx * ly / size_factor **2
>>> rgb_test[:,:,1] = (X - lx / 2 + lx*offset_factor) ** 2 + \
... (Y - ly / 2 - ly*offset_factor) ** 2 < \
... lx * ly / size_factor **2
>>> rgb_test[:,:,2] = (X - lx / 2) ** 2 + \
... (Y - ly / 2 + ly*offset_factor) ** 2 \
... < lx * ly / size_factor **2
>>> rgb_test *= 2**16 - 1
>>> s = hs.signals.Signal1D(rgb_test)
>>> s.change_dtype("uint16")
>>> s
<Signal1D, title: , dimensions: (1024, 1024|3)>
>>> s.change_dtype("rgb16")
>>> s
<Signal2D, title: , dimensions: (|1024, 1024)>
>>> s.plot()
RGB data type example.
Transposing (changing signal spaces)
New in version 1.1.
transpose() method changes how the dataset
dimensions are interpreted (as signal or navigation axes). By default is
swaps the signal and navigation axes. For example:
>>> s = hs.signals.Signal1D(np.zeros((4,5,6)))
>>> s
<Signal1D, title: , dimensions: (5, 4|6)>
>>> s.transpose()
<Signal2D, title: , dimensions: (6|4, 5)>
For T() is a shortcut for the default behaviour:
>>> s = hs.signals.Signal1D(np.zeros((4,5,6))).T
<Signal2D, title: , dimensions: (6|4, 5)>
The method accepts both explicit axes to keep in either space, or just a number
of axes required in one space (just one number can be specified, as the other
is defined as “all other axes”). When axes order is not explicitly defined,
they are “rolled” from one space to the other as if the <navigation axes |
signal axes > wrap a circle. The example below should help clarifying this.
>>> # just create a signal with many distinct dimensions
>>> s = hs.signals.BaseSignal(np.random.rand(1,2,3,4,5,6,7,8,9))
>>> s
<BaseSignal, title: , dimensions: (|9, 8, 7, 6, 5, 4, 3, 2, 1)>
>>> s.transpose(signal_axes=5) # roll to leave 5 axes in signal space
<BaseSignal, title: , dimensions: (4, 3, 2, 1|9, 8, 7, 6, 5)>
>>> s.transpose(navigation_axes=3) # roll leave 3 axes in navigation space
<BaseSignal, title: , dimensions: (3, 2, 1|9, 8, 7, 6, 5, 4)>
>>> # 3 explicitly defined axes in signal space
>>> s.transpose(signal_axes=[0, 2, 6])
<BaseSignal, title: , dimensions: (8, 6, 5, 4, 2, 1|9, 7, 3)>
>>> # A mix of two lists, but specifying all axes explicitly
>>> # The order of axes is preserved in both lists
>>> s.transpose(navigation_axes=[1, 2, 3, 4, 5, 8], signal_axes=[0, 6, 7])
<BaseSignal, title: , dimensions: (8, 7, 6, 5, 4, 1|9, 3, 2)>
A convenience functions transpose() is available to operate on
many signals at once, for example enabling plotting any-dimension signals
trivially:
>>> s2 = hs.signals.BaseSignal(np.random.rand(2, 2)) # 2D signal
>>> s3 = hs.signals.BaseSignal(np.random.rand(3, 3, 3)) # 3D signal
>>> s4 = hs.signals.BaseSignal(np.random.rand(4, 4, 4, 4)) # 4D signal
>>> hs.plot.plot_images(hs.transpose(s2, s3, s4, signal_axes=2))
The transpose() method accepts keyword argument
optimize, which is False by default, meaning modifying the output
signal data always modifies the original data i.e. the data is just a view
of the original data. If True, the method ensures the data in memory is
stored in the most efficient manner for iterating by making a copy of the data
if required, hence modifying the output signal data not always modifies the
original data.
The convenience methods as_signal1D() and
as_signal2D() internally use
transpose(), but always optimize the data
for iteration over the navigation axes if required. Hence, these methods do not
always return a view of the original data. If a copy of the data is required
use
deepcopy() on the output of any of these
methods e.g.:
>>> hs.signals.Signal1D(np.zeros((4,5,6))).T.deepcopy()
<Signal2D, title: , dimensions: (6|4, 5)>
Applying apodization window
Apodization window (also known as apodization function) can be applied to a signal
using apply_apodization() method. By default standard
Hann window is used:
>>> s = hs.signals.Signal1D(np.ones(1000))
>>> sa = s.apply_apodization()
>>> sa.metadata.General.title = 'Hann window'
>>> sa.plot()
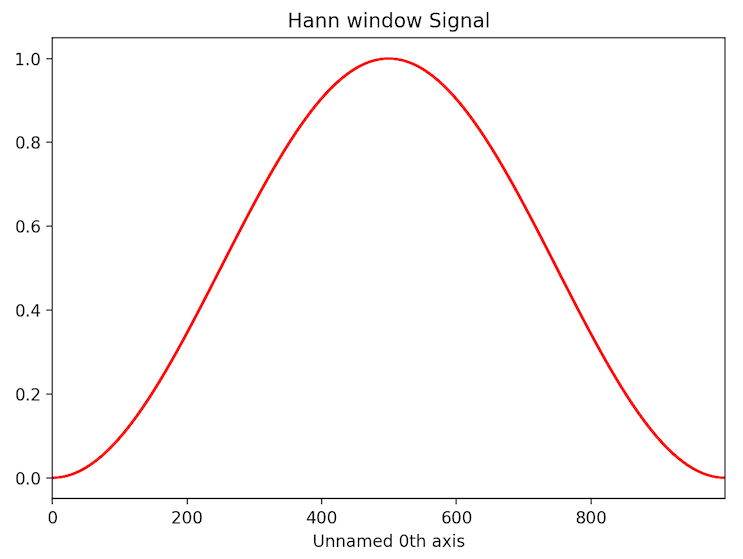
Higher order Hann window can be used in order to keep larger fraction of intensity of original signal.
This can be done providing an integer number for the order of the window through
keyword argument hann_order. (The last one works only together with default value of window argument
or with window='hann'.)
>>> im = hs.datasets.example_signals.reference_hologram().isig[:200, :200]
>>> ima = im.apply_apodization(window='hann', hann_order=3)
>>> hs.plot.plot_images([im, ima], vmax=3000, tight_layout=True)
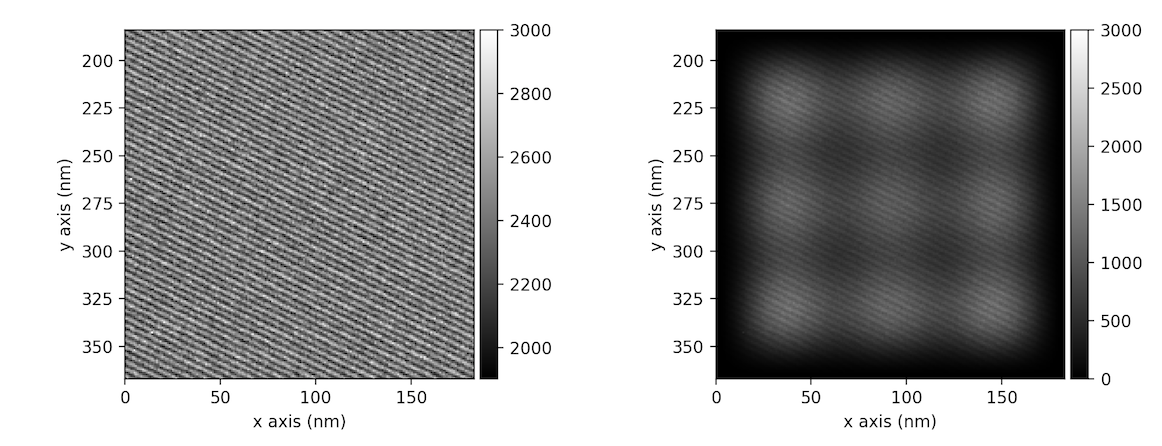
In addition to Hann window also Hamming or Tukey windows can be applied using window attribute
selecting 'hamming' or 'tukey' respectively.
The shape of Tukey window can be adjusted using parameter alpha
provided through tukey_alpha keyword argument (only used when window='tukey').
The parameter represents the fraction of the window inside the cosine tapered region,
i.e. smaller is alpha larger is the middle flat region where the original signal
is preserved. If alpha is one, the Tukey window is equivalent to a Hann window.
(Default value is 0.5)
Apodization can be applied in place by setting keyword argument inplace to True.
In this case method will not return anything.
Basic statistical analysis
get_histogram() computes the histogram and
conveniently returns it as signal instance. It provides methods to
calculate the bins. print_summary_statistics()
prints the five-number summary statistics of the data.
These two methods can be combined with
get_current_signal() to compute the histogram or
print the summary statistics of the signal at the current coordinates, e.g:
>>> s = hs.signals.EELSSpectrum(np.random.normal(size=(10,100)))
>>> s.print_summary_statistics()
Summary statistics
------------------
mean: 0.021
std: 0.957
min: -3.991
Q1: -0.608
median: 0.013
Q3: 0.652
max: 2.751
>>> s.get_current_signal().print_summary_statistics()
Summary statistics
------------------
mean: -0.019
std: 0.855
min: -2.803
Q1: -0.451
median: -0.038
Q3: 0.484
max: 1.992
Histogram of different objects can be compared with the functions
plot_histograms() (see
visualisation for the plotting options). For example,
with histograms of several random chi-square distributions:
>>> img = hs.signals.Signal2D([np.random.chisquare(i+1,[100,100]) for
... i in range(5)])
>>> hs.plot.plot_histograms(img,legend='auto')
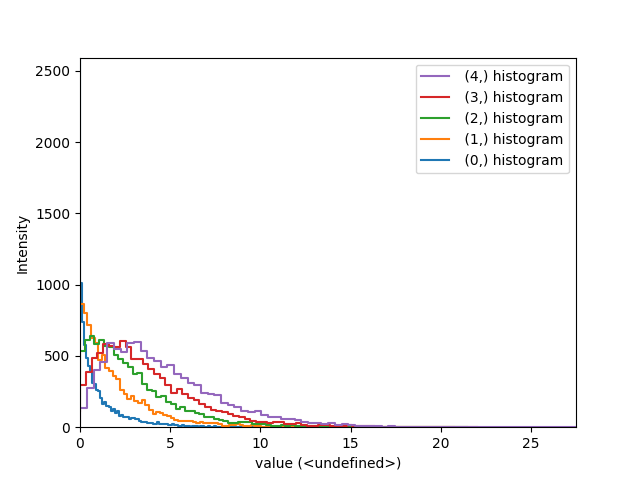
Comparing histograms.
Setting the noise properties
Some data operations require the data variance. Those methods use the
metadata.Signal.Noise_properties.variance attribute if it exists. You can
set this attribute as in the following example where we set the variance to be
10:
>>> s.metadata.Signal.set_item("Noise_properties.variance", 10)
You can also use the functions set_noise_variance()
and get_noise_variance() for convenience:
>>> s.set_noise_variance(10)
>>> s.get_noise_variance()
10
For heteroscedastic noise the variance attribute must be a
BaseSignal. Poissonian noise is a common case of
heteroscedastic noise where the variance is equal to the expected value. The
estimate_poissonian_noise_variance()
method can help setting the variance of data with
semi-Poissonian noise. With the default arguments, this method simply sets the
variance attribute to the given expected_value. However, more generally
(although the noise is not strictly Poissonian), the variance may be
proportional to the expected value. Moreover, when the noise is a mixture of
white (Gaussian) and Poissonian noise, the variance is described by the
following linear model:
\[\mathrm{Var}[X] = (a * \mathrm{E}[X] + b) * c\]
Where a is the gain_factor, b is the gain_offset (the Gaussian
noise variance) and c the correlation_factor. The correlation
factor accounts for correlation of adjacent signal elements that can
be modelled as a convolution with a Gaussian point spread function.
estimate_poissonian_noise_variance() can be used to
set the noise properties when the variance can be described by this linear
model, for example:
>>> s = hs.signals.Spectrum(np.ones(100))
>>> s.add_poissonian_noise()
>>> s.metadata
├── General
│ └── title =
└── Signal
└── signal_type =
>>> s.estimate_poissonian_noise_variance()
>>> s.metadata
├── General
│ └── title =
└── Signal
├── Noise_properties
│ ├── Variance_linear_model
│ │ ├── correlation_factor = 1
│ │ ├── gain_factor = 1
│ │ └── gain_offset = 0
│ └── variance = <SpectrumSimulation, title: Variance of , dimensions: (|100)>
└── signal_type =
Speeding up operations
Reusing a Signal for output
Many signal methods create and return a new signal. For fast operations, the
new signal creation time is non-negligible. Also, when the operation is
repeated many times, for example in a loop, the cumulative creation time can
become significant. Therefore, many operations on
BaseSignal accept an optional argument out. If an
existing signal is passed to out, the function output will be placed into
that signal, instead of being returned in a new signal. The following example
shows how to use this feature to slice a BaseSignal. It is
important to know that the BaseSignal instance passed in
the out argument must be well-suited for the purpose. Often this means that
it must have the same axes and data shape as the
BaseSignal that would normally be returned by the
operation.
>>> s = hs.signals.Signal1D(np.arange(10))
>>> s_sum = s.sum(0)
>>> s_sum.data
array([45])
>>> s.isig[:5].sum(0, out=s_sum)
>>> s_sum.data
array([10])
>>> s_roi = s.isig[:3]
>>> s_roi
<Signal1D, title: , dimensions: (|3)>
>>> s.isig.__getitem__(slice(None, 5), out=s_roi)
>>> s_roi
<Signal1D, title: , dimensions: (|5)>
Handling complex data
The HyperSpy ComplexSignal signal class
and its subclasses for 1-dimensional and 2-dimensional data allow the user to
access complex properties like the real and imag parts of the data or the
amplitude (also known as the modulus) and phase (also known as angle or
argument) directly. Getting and setting those properties can be done as
follows:
>>> real = s.real # real is a new HS signal accessing the same data
>>> s.real = new_real # new_real can be an array or signal
>>> imag = s.imag # imag is a new HS signal accessing the same data
>>> s.imag = new_imag # new_imag can be an array or signal
It is important to note that data passed to the constructor of a
ComplexSignal (or to a subclass), which
is not already complex, will be converted to the numpy standard of
np.complex/np.complex128. data which is already complex will be passed
as is.
To transform a real signal into a complex one use:
>>> s.change_dtype(complex)
Changing the dtype of a complex signal to something real is not clearly
defined and thus not directly possible. Use the real, imag,
amplitude or phase properties instead to extract the real data that is
desired.
Calculate the angle / phase / argument
The angle() function
can be used to calculate the angle, which is equivalent to using the phase
property if no argument is used. If the data is real, the angle will be 0 for
positive values and 2$pi$ for negative values. If the deg parameter is set
to True, the result will be given in degrees, otherwise in rad (default).
The underlying function is the numpy.angle() function.
angle() will return
an appropriate HyperSpy signal.
Phase unwrapping
With the unwrapped_phase()
method the complex phase of a signal can be unwrapped and returned as a new signal.
The underlying method is skimage.restoration.unwrap_phase(), which
uses the algorithm described in [Herraez].
Calculate and display Argand diagram
Sometimes it is convenient to visualize a complex signal as a plot of its
imaginary part versus real one. In this case so called Argand diagrams can
be calculated using argand_diagram()
method, which returns the plot as a Signal2D.
Optional arguments size and display_range can be used to change the
size (and therefore resolution) of the plot and to change the range for the
display of the plot respectively. The last one is especially useful in order to
zoom into specific regions of the plot or to limit the plot in case of noisy
data points.
An example of calculation of Aragand diagram is shown for electron holography data.
Add a linear phase ramp
For 2-dimensional complex images, a linear phase ramp can be added to the
signal via the
add_phase_ramp() method.
The parameters ramp_x and ramp_y dictate the slope of the ramp in x-
and y direction, while the offset is determined by the offset parameter.
The fulcrum of the linear ramp is at the origin and the slopes are given in
units of the axis with the according scale taken into account. Both are
available via the AxesManager of the signal.
New in version 1.7.
GPU support
GPU processing is supported thanks to the numpy dispatch mechanism of array functions
- read NEP-18
and NEP-35
for more information. It means that most HyperSpy functions will work on a GPU
if the data is a cupy.ndarray and the required functions are
implemented in cupy.
Note
GPU processing with hyperspy requires numpy>=1.20 and dask>=2021.3.0, to be able to use NEP-18 and NEP-35.
>>> import cupy as cp
>>> # Create a cupy array (on GPU device)
>>> data = cp.random.random(size=(20, 20, 100, 100))
>>> s = hs.signals.Signal2D(data)
>>> type(s.data)
... cupy._core.core.ndarray
Two convenience methods are available to transfer data between the host and the (GPU) device memory:
For lazy processing, see the corresponding section.