Fitting the model to the data#
To fit the model to the data at the current coordinates (e.g. to fit one
spectrum at a particular point in a spectrum-image), use
fit(). HyperSpy implements a number of
different optimization approaches, each of which can have particular
benefits and/or drawbacks depending on your specific application.
A good approach to choosing an optimization approach is to ask yourself
the question “Do you want to…”:
Apply bounds to your model parameter values?
Use gradient-based fitting algorithms to accelerate your fit?
Estimate the standard deviations of the parameter values found by the fit?
Fit your data in the least-squares sense, or use another loss function?
Find the global optima for your parameters, or is a local optima acceptable?
Optimization algorithms#
The following table summarizes the features of some of the optimizers currently available in HyperSpy, including whether they support parameter bounds, gradients and parameter error estimation. The “Type” column indicates whether the optimizers find a local or global optima.
Optimizer |
Bounds |
Gradients |
Errors |
Loss function |
Type |
Linear |
|---|---|---|---|---|---|---|
|
Yes |
Yes |
Yes |
Only |
local |
No |
|
Yes |
Yes |
Yes |
Only |
local |
No |
|
Yes |
Yes |
Yes |
Only |
local |
No |
|
Yes |
Yes |
Yes |
Only |
local |
No |
|
No |
No |
Yes [3] |
Only |
global |
Yes |
|
No |
No |
Yes [3] |
Only |
global |
Yes |
|
No |
No |
Yes [3] |
Only |
global |
Yes |
|
No |
No |
Yes [3] |
Only |
global |
Yes |
Yes [4] |
Yes [4] |
Yes |
All |
local |
No |
|
|
Yes |
No |
Yes |
All |
global |
No |
|
Yes |
No |
Yes |
All |
global |
No |
|
Yes |
No |
Yes |
All |
global |
No |
Footnotes
Loss functions#
HyperSpy supports a number of loss functions. The default is "ls",
i.e. the least-squares loss. For the vast majority of cases, this loss
function is appropriate, and has the additional benefit of supporting
parameter error estimation and goodness-of-fit
testing. However, if your data contains very low counts per pixel, or
is corrupted by outliers, the "ML-poisson" and "huber" loss
functions may be worth investigating.
Least squares with error estimation#
The following example shows how to perfom least squares optimization with
error estimation. First we create data consisting of a line
y = a*x + b with a = 1 and b = 100, and we then add Gaussian
noise to it:
>>> s = hs.signals.Signal1D(np.arange(100, 300, dtype='float32'))
>>> s.add_gaussian_noise(std=100)
To fit it, we create a model consisting of a
Polynomial component of order 1 and fit it
to the data.
>>> m = s.create_model()
>>> line = hs.model.components1D.Polynomial(order=1)
>>> m.append(line)
>>> m.fit()
Once the fit is complete, the optimized value of the parameters and their estimated standard deviation are stored in the following line attributes:
>>> line.a0.value
0.9924615648843765
>>> line.a1.value
103.67507406125888
>>> line.a0.std
0.11771053738516088
>>> line.a1.std
13.541061301257537
Warning
When the noise is heteroscedastic, only if the
metadata.Signal.Noise_properties.variance attribute of the
Signal1D instance is defined can
the parameter standard deviations be estimated accurately.
If the variance is not defined, the standard deviations are still computed, by setting variance equal to 1. However, this calculation will not be correct unless an accurate value of the variance is provided. See Setting the noise properties for more information.
Weighted least squares with error estimation#
In the following example, we add Poisson noise to the data instead of Gaussian noise, and proceed to fit as in the previous example.
>>> s = hs.signals.Signal1D(np.arange(300))
>>> s.add_poissonian_noise()
>>> m = s.create_model()
>>> line = hs.model.components1D.Polynomial(order=1)
>>> m.append(line)
>>> m.fit()
>>> line.a0.value
-0.7262000522775925
>>> line.a1.value
1.0086925334859176
>>> line.a0.std
1.4141418570079
>>> line.a1.std
0.008185019194679451
Because the noise is heteroscedastic, the least squares optimizer estimation is biased. A more accurate result can be obtained with weighted least squares, where the weights are proportional to the inverse of the noise variance. Although this is still biased for Poisson noise, it is a good approximation in most cases where there are a sufficient number of counts per pixel.
>>> exp_val = hs.signals.Signal1D(np.arange(300)+1)
>>> s.estimate_poissonian_noise_variance(expected_value=exp_val)
>>> line.estimate_parameters(s, 10, 250)
True
>>> m.fit()
>>> line.a0.value
-0.6666008600519397
>>> line.a1.value
1.017145603577098
>>> line.a0.std
0.8681360488613021
>>> line.a1.std
0.010308732161043038
Warning
When the attribute metadata.Signal.Noise_properties.variance
is defined, the behaviour is to perform a weighted least-squares
fit using the inverse of the noise variance as the weights.
In this scenario, to then disable weighting, you will need to unset
the attribute. You can achieve this with
set_noise_variance():
>>> m.signal.set_noise_variance(None) # This will now be an unweighted fit
>>> m.fit()
>>> line.a0.value
-1.9711403542163477
>>> line.a1.value
1.0258716193502546
Poisson maximum likelihood estimation#
To avoid biased estimation in the case of data corrupted by Poisson noise with very few counts, we can use Poisson maximum likelihood estimation (MLE) instead. This is an unbiased estimator for Poisson noise. To perform MLE, we must use a general, non-linear optimizer from the table above, such as Nelder-Mead or L-BFGS-B:
>>> m.fit(optimizer="Nelder-Mead", loss_function="ML-poisson")
>>> line.a0.value
0.00025567973144090695
>>> line.a1.value
1.0036866523183754
Huber loss function#
HyperSpy also implements the Huber loss function, which is typically less sensitive to outliers in the data compared to the least-squares loss. Again, we need to use one of the general non-linear optimization algorithms:
>>> m.fit(optimizer="Nelder-Mead", loss_function="huber")
Custom loss functions#
As well as the built-in loss functions described above, a custom loss function can be passed to the model:
>>> def my_custom_function(model, values, data, weights=None):
... """
... Parameters
... ----------
... model : Model instance
... the model that is fitted.
... values : np.ndarray
... A one-dimensional array with free parameter values suggested by the
... optimizer (that are not yet stored in the model).
... data : np.ndarray
... A one-dimensional array with current data that is being fitted.
... weights : {np.ndarray, None}
... An optional one-dimensional array with parameter weights.
...
... Returns
... -------
... score : float
... A signle float value, representing a score of the fit, with
... lower values corresponding to better fits.
... """
... # Almost any operation can be performed, for example:
... # First we store the suggested values in the model
... model.fetch_values_from_array(values)
...
... # Evaluate the current model
... cur_value = model(onlyactive=True)
...
... # Calculate the weighted difference with data
... if weights is None:
... weights = 1
... difference = (data - cur_value) * weights
...
... # Return squared and summed weighted difference
... return (difference**2).sum()
>>> # We must use a general non-linear optimizer
>>> m.fit(optimizer='Nelder-Mead', loss_function=my_custom_function)
If the optimizer requires an analytical gradient function, it can be similarly passed, using the following signature:
>>> def my_custom_gradient_function(model, values, data, weights=None):
... """
... Parameters
... ----------
... model : Model instance
... the model that is fitted.
... values : np.ndarray
... A one-dimensional array with free parameter values suggested by the
... optimizer (that are not yet stored in the model).
... data : np.ndarray
... A one-dimensional array with current data that is being fitted.
... weights : {np.ndarray, None}
... An optional one-dimensional array with parameter weights.
...
... Returns
... -------
... gradients : np.ndarray
... a one-dimensional array of gradients, the size of `values`,
... containing each parameter gradient with the given values
... """
... # As an example, estimate maximum likelihood gradient:
... model.fetch_values_from_array(values)
... cur_value = model(onlyactive=True)
...
... # We use in-built jacobian estimation
... jac = model._jacobian(values, data)
...
... return -(jac * (data / cur_value - 1)).sum(1)
>>> # We must use a general non-linear optimizer again
>>> m.fit(optimizer='L-BFGS-B',
... loss_function=my_custom_function,
... grad=my_custom_gradient_function)
Note
Estimation of the parameter errors is not currently supported for custom loss functions.
Using gradient information#
Added in version 1.6: grad="analytical" and grad="fd" keyword arguments
Optimization algorithms that take into account the gradient of the loss function will often out-perform so-called “derivative-free” optimization algorithms in terms of how rapidly they converge to a solution. HyperSpy can use analytical gradients for model-fitting, as well as numerical estimates of the gradient based on finite differences.
If all the components in the model support analytical gradients,
you can pass grad="analytical" in order to use this information
when fitting. The results are typically more accurate than an
estimated gradient, and the optimization often runs faster since
fewer function evaluations are required to calculate the gradient.
Following the above examples:
>>> m = s.create_model()
>>> line = hs.model.components1D.Polynomial(order=1)
>>> m.append(line)
>>> # Use a 2-point finite-difference scheme to estimate the gradient
>>> m.fit(grad="fd", fd_scheme="2-point")
>>> # Use the analytical gradient
>>> m.fit(grad="analytical")
>>> # Huber loss and Poisson MLE functions
>>> # also support analytical gradients
>>> m.fit(grad="analytical", loss_function="huber")
>>> m.fit(grad="analytical", loss_function="ML-poisson")
Note
Analytical gradients are not yet implemented for the
Model2D class.
Bounded optimization#
Non-linear optimization can sometimes fail to converge to a good optimum, especially if poor starting values are provided. Problems of ill-conditioning and non-convergence can be improved by using bounded optimization.
All components’ parameters have the attributes parameter.bmin and
parameter.bmax (“bounded min” and “bounded max”). When fitting using the
bounded=True argument by m.fit(bounded=True) or m.multifit(bounded=True),
these attributes set the minimum and maximum values allowed for parameter.value.
Currently, not all optimizers support bounds - see the
table above. In the following example, a Gaussian
histogram is fitted using a Gaussian
component using the Levenberg-Marquardt (“lm”) optimizer and bounds
on the centre parameter.
>>> s = hs.signals.BaseSignal(np.random.normal(loc=10, scale=0.01,
... size=100000)).get_histogram()
>>> s.axes_manager[-1].is_binned = True
>>> m = s.create_model()
>>> g1 = hs.model.components1D.Gaussian()
>>> m.append(g1)
>>> g1.centre.value = 7
>>> g1.centre.bmin = 7
>>> g1.centre.bmax = 14
>>> m.fit(optimizer="lm", bounded=True)
>>> m.print_current_values()
Model1D: histogram
Gaussian: Gaussian
Active: True
Parameter Name | Free | Value | Std | Min | Max
============== | ===== | ========== | ========== | ========== | ==========
A | True | 99997.3481 | 232.333693 | 0.0 | None
sigma | True | 0.00999184 | 2.68064163 | None | None
centre | True | 9.99980788 | 2.68064070 | 7.0 | 14.0
Linear least squares#
Added in version 1.7.
Linear fitting can be used to address some of the drawbacks of non-linear optimization:
it doesn’t suffer from the starting parameters issue, which can sometimes be problematic with nonlinear fitting. Since linear fitting uses linear algebra to find the solution (find the parameter values of the model), the solution is a unique solution, while nonlinear optimization uses an iterative approach and therefore relies on the initial values of the parameters.
it is fast, because i) in favorable situations, the signal can be fitted in a vectorized fashion, i.e. the signal is fitted in a single run instead of iterating over the navigation dimension; ii) it is not iterative, i.e. it does the calculation only one time instead of 10-100 iterations, depending on how quickly the non-linear optimizer will converge.
However, linear fitting can only fit linear models and will not be able to fit parameters which vary non-linearly.
A component is considered linear when its free parameters scale the component only
in the y-axis. For the exemplary function y = a*x**b, a is a linear parameter, whilst b
is not. If b.free = False, then the component is linear.
Components can also be made up of several linear parts. For instance,
the 2D-polynomial y = a*x**2+b*y**2+c*x+d*y+e is entirely linear.
Note
After creating a model with values for the nonlinear parameters, a quick way to set
all nonlinear parameters to be free = False is to use m.set_parameters_not_free(only_nonlinear=True)
To check if a parameter is linear, use the model or component method
print_current_values(). For a component to be
considered linear, it can hold only one free parameter, and that parameter
must be linear.
If all components in a model are linear, then a linear optimizer can be used to solve the problem as a linear regression problem! This can be done using two approaches:
the standard pixel-by-pixel approach as used by the nonlinear optimizers
fit the entire dataset in one vectorised operation, which will be much faster (up to 1000 times). However, there is a caveat: all fixed parameters must have the same value across the dataset in order to avoid creating a very large array whose size will scale with the number of different values of the non-free parameters.
Note
A good example of a linear model in the electron-microscopy field is an Energy-Dispersive
X-ray Spectroscopy (EDS) dataset, which typically consists of a polynomial background and
Gaussian peaks with well-defined energy (Gaussian.centre) and peak widths
(Gaussian.sigma). This dataset can be fit extremely fast with a linear optimizer.
There are several implementations of linear least squares fitting in HyperSpy:
'lstsq': least squares usingnumpy.linalg.lstsq(), ordask.array.linalg.lstsq()for lazy signals,'ols': ordinary least squares, usingsklearn.linear_model.LinearRegression,'nnls': least squares with positive constraints on the coefficients usingsklearn.linear_model.LinearRegression,'ridge': least square supporting regularisation usingsklearn.linear_model.Ridge. The parameteralphacontrols the regularization strength and can significantly affect the results.
See the corresponding documentation in scikit-learn
or numpy.linalg.lstsq() for passing parameters to fit() or
multifit().
Only the 'lstsq' optimizer supports lazy signals.
As for non-linear least squares fitting, weighted least squares are supported.
In the following example, we first generate a 300x300 navigation signal of varying total intensity,
and then populate it with an EDS spectrum at each point. The signal can be fitted with a polynomial
background and a Gaussian for each peak. Hyperspy automatically adds these to the model, and fixes
the centre and sigma parameters to known values. Fitting this model with a non-linear optimizer
can about half an hour on a decent workstation. With a linear optimizer, it takes seconds.
>>> nav = hs.signals.Signal2D(np.random.random((300, 300))).T
>>> s = exspy.data.EDS_TEM_FePt_nanoparticles() * nav
>>> m = s.create_model()
>>> m.multifit(optimizer='lstsq')
Standard errors for the parameters are by default not calculated when the dataset
is fitted in vectorized fashion, because it has large memory requirement.
If errors are required, either pass calculate_errors=True as an argument
to multifit(), or rerun
multifit() with a nonlinear optimizer,
which should run fast since the parameters are already optimized.
None of the linear optimizers currently support bounds.
Optimization results#
After fitting the model, details about the optimization
procedure, including whether it finished successfully,
are returned as scipy.optimize.OptimizeResult object,
according to the keyword argument return_info=True.
These details are often useful for diagnosing problems such
as a poorly-fitted model or a convergence failure.
You can also access the object as the fit_output attribute:
>>> m.fit()
>>> type(m.fit_output)
<scipy.optimize.OptimizeResult object>
You can also print this information using the
print_info keyword argument:
# Print the info to stdout
>>> m.fit(optimizer="L-BFGS-B", print_info=True) # doctest: +SKIP
Fit info:
optimizer=L-BFGS-B
loss_function=ls
bounded=False
grad="fd"
Fit result:
hess_inv: <3x3 LbfgsInvHessProduct with dtype=float64>
message: b'CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH'
nfev: 168
nit: 32
njev: 42
status: 0
success: True
x: array([ 9.97614503e+03, -1.10610734e-01, 1.98380701e+00])
Goodness of fit#
The chi-squared, reduced chi-squared and the degrees of freedom are
computed automatically when fitting a (weighted) least-squares model
(i.e. only when loss_function="ls"). They are stored as signals, in the
chisq, red_chisq and
dof attributes of the model respectively.
Warning
Unless metadata.Signal.Noise_properties.variance contains
an accurate estimation of the variance of the data, the chi-squared and
reduced chi-squared will not be computed correctly. This is true for both
homocedastic and heteroscedastic noise.
Visualizing the model#
To visualise the result use the plot() method:
>>> m.plot() # Visualise the results
By default only the full model line is displayed in the plot. In addition, it
is possible to display the individual components by calling
enable_plot_components() or directly using
plot():
>>> m.plot(plot_components=True) # Visualise the results
To disable this feature call
disable_plot_components().
Added in version 1.4: plot() keyword arguments
All extra keyword arguments are passed to the plot()
method of the corresponding signal object. The following example plots the
model signal figure but not its navigator:
>>> m.plot(navigator=False)
By default the model plot is automatically updated when any parameter value
changes. It is possible to suspend this feature with
suspend_update().
Setting the initial parameters#
Non-linear optimization often requires setting sensible starting parameters. This can be done by plotting the model and adjusting the parameters by hand.
Changed in version 1.3: All notebook_interaction methods renamed to gui().
The notebook_interaction methods were removed in 2.0.
If running in a Jupyter Notebook, interactive widgets can be used to
conveniently adjust the parameter values by running
gui() for BaseModel,
Component and
Parameter.
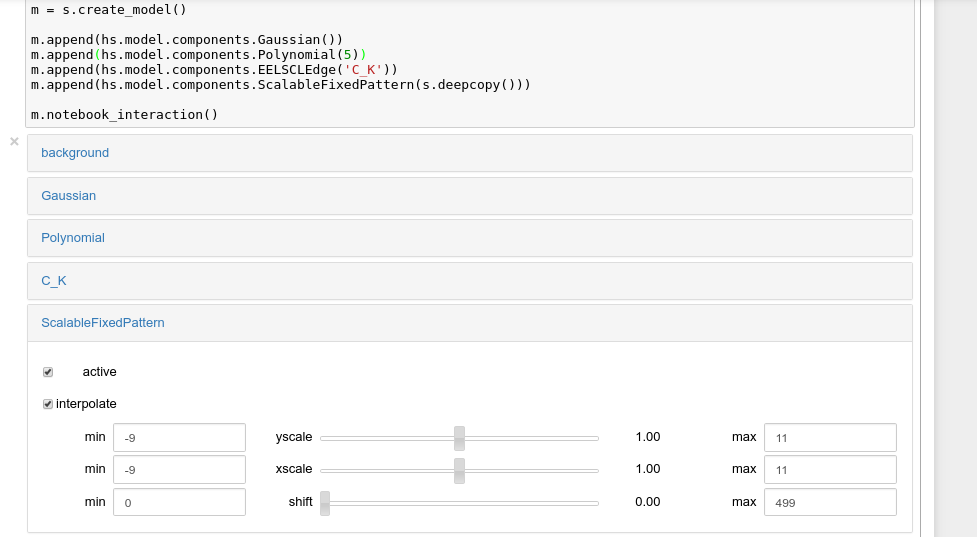
Interactive widgets for the full model in a Jupyter notebook. Drag the sliders to adjust current parameter values. Typing different minimum and maximum values changes the boundaries of the slider.#
Also, enable_adjust_position() provides an
interactive way of setting the position of the components with a
well-defined position.
disable_adjust_position() disables the tool.
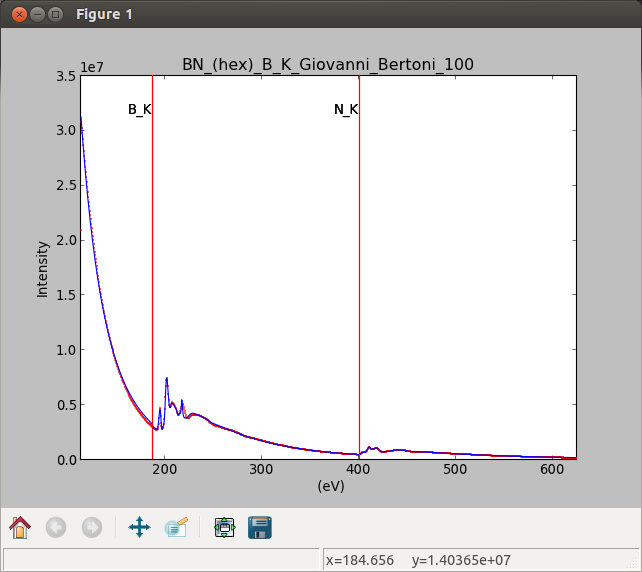
Interactive component position adjustment tool. Drag the vertical lines to set the initial value of the position parameter.#
Exclude data from the fitting process#
The following BaseModel methods can be used to exclude
undesired spectral channels from the fitting process:
The example below shows how a boolean array can be easily created from the
signal and how the isig syntax can be used to define the signal range.
>>> # Create a sample 2D gaussian dataset
>>> g = hs.model.components2D.Gaussian2D(
... A=1, centre_x=-5.0, centre_y=-5.0, sigma_x=1.0, sigma_y=2.0,)
>>> scale = 0.1
>>> x = np.arange(-10, 10, scale)
>>> y = np.arange(-10, 10, scale)
>>> X, Y = np.meshgrid(x, y)
>>> im = hs.signals.Signal2D(g.function(X, Y))
>>> im.axes_manager[0].scale = scale
>>> im.axes_manager[0].offset = -10
>>> im.axes_manager[1].scale = scale
>>> im.axes_manager[1].offset = -10
>>> m = im.create_model() # Model initialisation
>>> gt = hs.model.components2D.Gaussian2D()
>>> m.append(gt)
>>> m.set_signal_range(-7, -3, -9, -1) # Set signal range
>>> m.fit()
Alternatively, create a boolean signal of the same shape
as the signal space of im
>>> signal_mask = im > 0.01
>>> m.set_signal_range_from_mask(signal_mask.data) # Set signal range
>>> m.fit()
Fitting multidimensional datasets#
To fit the model to all the elements of a multidimensional dataset, use
multifit():
>>> m.multifit() # warning: this can be a lengthy process on large datasets
multifit() fits the model at the first position,
stores the result of the fit internally and move to the next position until
reaching the end of the dataset.
Note
Sometimes this method can fail, especially in the case of a TEM spectrum image of a particle surrounded by vacuum (since in that case the top-left pixel will typically be an empty signal).
To get sensible starting parameters, you can do a single
fit() after changing the active position
within the spectrum image (either using the plotting GUI or by directly
modifying s.axes_manager.indices as in Setting axis properties).
After doing this, you can initialize the model at every pixel to the
values from the single pixel fit using m.assign_current_values_to_all(),
and then use multifit() to perform the fit over
the entire spectrum image.
Added in version 1.6: New optional fitting iteration path “serpentine”
Added in version 2.0: New default iteration path for fitting is “serpentine”`
In HyperSpy, curve fitting on a multidimensional dataset happens in the following manner: Pixels are fit along the row from the first index in the first row, and once the last pixel in the row is reached, one proceeds in reverse order from the last index in the second row. This procedure leads to a serpentine pattern, as seen on the image below. The serpentine pattern supports n-dimensional navigation space, so the first index in the second frame of a three-dimensional navigation space will be at the last position of the previous frame.
An alternative scan pattern would be the 'flyback' scheme, where the map is
iterated through row by row, always starting from the first index. This pattern
can be explicitly set using the multifit()
iterpath='flyback' argument. However, the 'serpentine' strategy is
usually more robust, as it always moves on to a neighbouring pixel and the fitting
procedure uses the fit result of the previous pixel as the starting point for the
next. A common problem in the 'flyback' pattern is that the fitting fails
going from the end of one row to the beginning of the next, as the spectrum can
change abruptly.
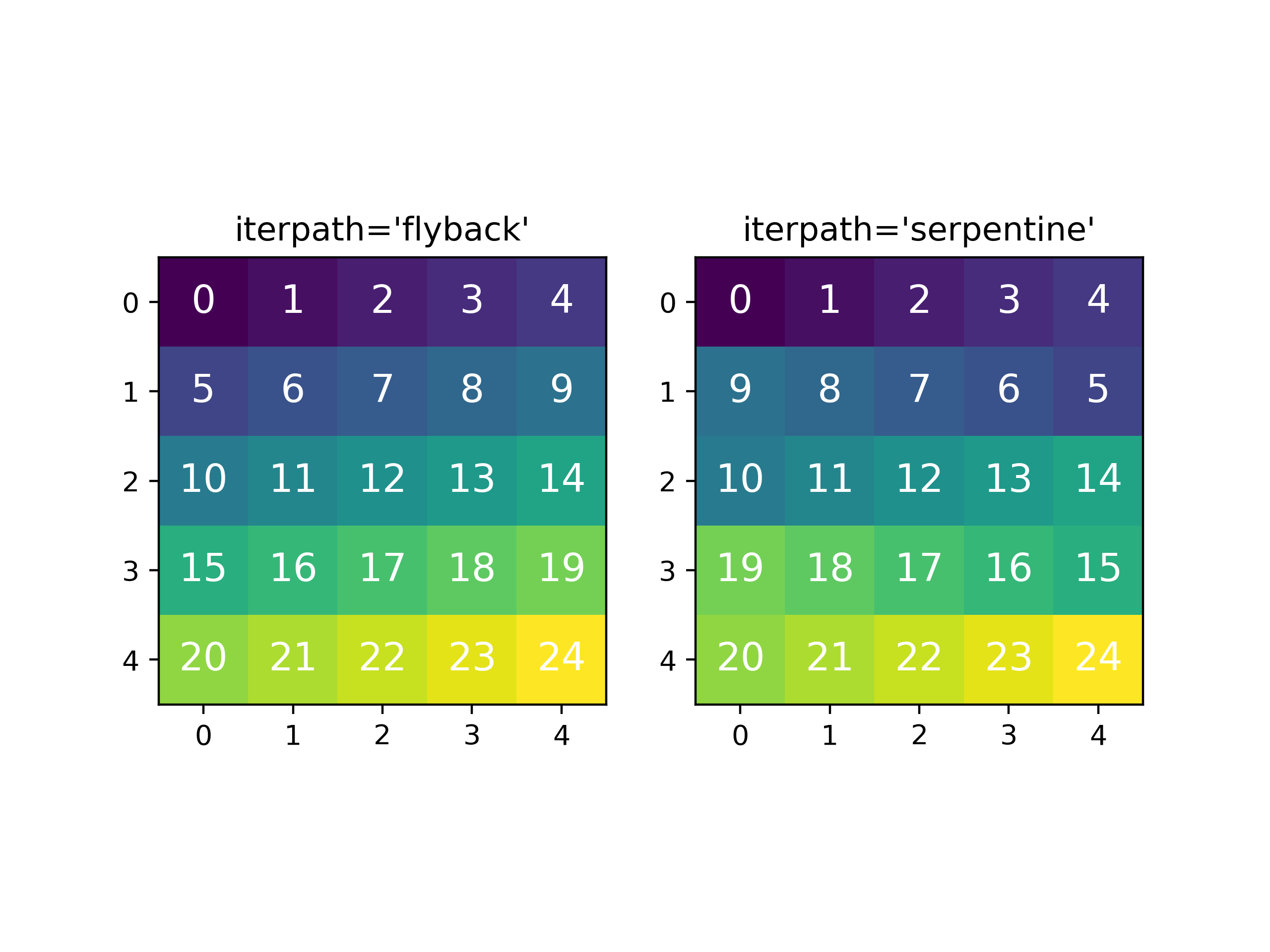
Comparing the scan patterns generated by the 'flyback' and 'serpentine'
iterpath options for a 2D navigation space. The pixel intensity and number
refers to the order that the signal is fitted in.#
In addition to 'serpentine' and 'flyback', iterpath can take as
argument any list or array of indices, or a generator of such, as explained in
the Iterating AxesManager section.
Sometimes one may like to store and fetch the value of the parameters at a
given position manually. This is possible using
store_current_values() and
fetch_stored_values().
Visualising the result of the fit#
The BaseModel plot_results(),
Component plot() and
Parameter plot() methods
can be used to visualise the result of the fit when fitting multidimensional
datasets.
Compute model statistics#
HyperSpy provides a method to compute and print summary statistics of all parameters of each component in a model. This is especially useful for inspecting parameter values after fitting a map of spectra using multifit, as it allows evaluating mean, standard deviation, minimum, and maximum across all navigation points.
>>> x = np.linspace(0, 20, 200)
>>> y = (
... 3 * np.exp(-((x - 5) ** 2) / (2 * 0.5**2))
... + 2 * np.exp(-((x - 10) ** 2) / (2 * 1.0**2))
... + 4 * np.exp(-((x - 15) ** 2) / (2 * 0.8**2))
... )
>>> s = hs.signals.Signal1D(y)
>>> m = s.create_model()
>>> gauss1 = hs.model.components1D.Gaussian()
>>> gauss2 = hs.model.components1D.Gaussian()
>>> gauss3 = hs.model.components1D.Gaussian()
>>> lorenz1 = hs.model.components1D.Lorentzian()
>>> lorenz2 = hs.model.components1D.Lorentzian()
>>> m.extend([gauss1, gauss2, gauss3, lorenz1, lorenz2])
>>> m.multifit()
>>> m.print_model_statistics()
The output includes the mean, standard deviation, minimum, and maximum for each parameter of each component. Thresholds can optionally be applied to filter the values considered in the statistics.