hyperspy._signals.complex_signal module

class hyperspy._signals.complex_signal.ComplexSignal(*args, **kwargs)

Bases: hyperspy._signals.complex_signal.ComplexSignal_mixin, hyperspy.signal.BaseSignal

Create a Signal from a numpy array.

Parameters

data (numpy.ndarray) – The signal data. It can be an array of any dimensions.
axes (dict, optional) – Dictionary to define the axes (see the documentation of the AxesManager class for more details).
attributes (dict, optional) – A dictionary whose items are stored as attributes.
metadata (dict, optional) – A dictionary containing a set of parameters that will to stores in the metadata attribute. Some parameters might be mandatory in some cases.
original_metadata (dict, optional) – A dictionary containing a set of parameters that will to stores in the original_metadata attribute. It typically contains all the parameters that has been imported from the original data file.

angle(deg=False)

Return the angle (also known as phase or argument). If the data is real, the angle is 0 for positive values and 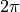$2\pi$ for negative values.

Parameters: deg (bool, optional) – Return angle in degrees if True, radians if False (default).
Returns: angle – The counterclockwise angle from the positive real axis on the complex plane, with dtype as numpy.float64.
Return type: HyperSpy signal

argand_diagram(size=[256, 256], range=None)

Calculate and plot Argand diagram of complex signal

Parameters

size ([int, int], optional) – Size of the Argand plot in pixels (Default: [256, 256])
range (array_like, shape(2,2) or shape(2,) optional) – The position of the edges of the diagram (if not specified explicitly in the bins parameters): [[xmin, xmax], [ymin, ymax]]. All values outside of this range will be considered outliers and not tallied in the histogram. (Default: None)

Returns

Argand diagram as Signal2D

Return type

argand_diagram

Examples

>>> import hyperspy.api as hs
>>> holo = hs.datasets.example_signals.object_hologram()
>>> ref = hs.datasets.example_signals.reference_hologram()
>>> w = holo.reconstruct_phase(ref)
>>> w.argand_diagram(range=[-3, 3]).plot()

class hyperspy._signals.complex_signal.ComplexSignal_mixin(*args, **kwargs)

Bases: object

BaseSignal subclass for complex data.

property amplitude: Get/set the amplitude of the data. Returns an appropriate HyperSpy signal.

angle(angle, deg=False)

Return the angle (also known as phase or argument). If the data is real, the angle is 0 for positive values and 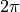$2\pi$ for negative values.

Parameters: deg (bool, optional) – Return angle in degrees if True, radians if False (default).
Returns: angle – The counterclockwise angle from the positive real axis on the complex plane, with dtype as numpy.float64.
Return type: HyperSpy signal

change_dtype(dtype)

Change the data type.

Parameters: dtype (str or dtype) – Typecode or data-type to which the array is cast. For complex signals only other complex dtypes are allowed. If real valued properties are required use real, imag, amplitude and phase instead.

property imag: Get/set imaginary part of the data. Returns an appropriate HyperSpy signal.

property phase: Get/set the phase of the data. Returns an appropriate HyperSpy signal.

plot(power_spectrum=False, representation='cartesian', same_axes=True, fft_shift=False, navigator='auto', axes_manager=None, norm='auto', **kwargs)

Plot the signal at the current coordinates.

For multidimensional datasets an optional figure, the “navigator”, with a cursor to navigate that data is raised. In any case it is possible to navigate the data using the sliders. Currently only signals with signal_dimension equal to 0, 1 and 2 can be plotted.

Parameters

power_spectrum (bool, default is False.) – If True, plot the power spectrum instead of the actual signal, if False, plot the real and imaginary parts of the complex signal.
representation ({'cartesian' or 'polar'}) – Determines if the real and imaginary part of the complex data is plotted (‘cartesian’, default), or if the amplitude and phase should be used (‘polar’).
same_axes (bool, default True) – If True (default) plot the real and imaginary parts (or amplitude and phase) in the same figure if the signal is one-dimensional.
fft_shift (bool, default False) – If True, shift the zero-frequency component. See numpy.fft.fftshift() for more details.
navigator (str, None, or BaseSignal (or subclass). Allowed string values are 'auto', 'slider', and 'spectrum'.) –
If 'auto':
- If navigation_dimension > 0, a navigator is provided to explore the data.
- If navigation_dimension is 1 and the signal is an image the navigator is a sum spectrum obtained by integrating over the signal axes (the image).
- If navigation_dimension is 1 and the signal is a spectrum the navigator is an image obtained by stacking all the spectra in the dataset horizontally.
- If navigation_dimension is > 1, the navigator is a sum image obtained by integrating the data over the signal axes.
- Additionally, if navigation_dimension > 2, a window with one slider per axis is raised to navigate the data.
- For example, if the dataset consists of 3 navigation axes X, Y, Z and one signal axis, E, the default navigator will be an image obtained by integrating the data over E at the current Z index and a window with sliders for the X, Y, and Z axes will be raised. Notice that changing the Z-axis index changes the navigator in this case.
- For lazy signals, the navigator will be calculated using the compute_navigator() method.
If 'slider':
- If navigation dimension > 0 a window with one slider per axis is raised to navigate the data.
If 'spectrum':
- If navigation_dimension > 0 the navigator is always a spectrum obtained by integrating the data over all other axes.
- Not supported for lazy signals, the 'auto' option will be used instead.
If None, no navigator will be provided.

Alternatively a BaseSignal (or subclass) instance can be provided. The navigation or signal shape must match the navigation shape of the signal to plot or the navigation_shape + signal_shape must be equal to the navigator_shape of the current object (for a dynamic navigator). If the signal dtype is RGB or RGBA this parameter has no effect and the value is always set to 'slider'.
axes_manager (None or AxesManager) – If None, the signal’s axes_manager attribute is used.
plot_markers (bool, default True) – Plot markers added using s.add_marker(marker, permanent=True). Note, a large number of markers might lead to very slow plotting.
navigator_kwds (dict) – Only for image navigator, additional keyword arguments for matplotlib.pyplot.imshow().
**kwargs (dict) – Only when plotting an image: additional (optional) keyword arguments for matplotlib.pyplot.imshow().

property real: Get/set the real part of the data. Returns an appropriate HyperSpy signal.

unwrapped_phase(wrap_around=False, seed=None, show_progressbar=None, parallel=None, max_workers=None)

Return the unwrapped phase as an appropriate HyperSpy signal.

Parameters

wrap_around (bool or sequence of bool, optional) – When an element of the sequence is True, the unwrapping process will regard the edges along the corresponding axis of the image to be connected and use this connectivity to guide the phase unwrapping process. If only a single boolean is given, it will apply to all axes. Wrap around is not supported for 1D arrays.
seed (int, optional) – Unwrapping 2D or 3D images uses random initialization. This sets the seed of the PRNG to achieve deterministic behavior.
show_progressbar (None or bool) – If True, display a progress bar. If None, the default from the preferences settings is used.
parallel (None or bool) – If True, perform computation in parallel using multithreading. If None, the default from the preferences settings is used. The number of threads is controlled by the max_workers argument.
max_workers (None or int) – Maximum number of threads used when parallel=True. If None, defaults to min(32, os.cpu_count()).

Returns

phase_image – Unwrapped phase.

Return type

BaseSignal subclass

Notes

Uses the unwrap_phase() function from skimage. The algorithm is based on Miguel Arevallilo Herraez, David R. Burton, Michael J. Lalor, and Munther A. Gdeisat, “Fast two-dimensional phase-unwrapping algorithm based on sorting by reliability following a noncontinuous path”, Journal Applied Optics, Vol. 41, No. 35, pp. 7437, 2002

class hyperspy._signals.complex_signal.LazyComplexSignal(*args, **kwargs)

Bases: hyperspy._signals.complex_signal.ComplexSignal, hyperspy._signals.lazy.LazySignal

Create a Signal from a numpy array.

Parameters

data (numpy.ndarray) – The signal data. It can be an array of any dimensions.
axes (dict, optional) – Dictionary to define the axes (see the documentation of the AxesManager class for more details).
attributes (dict, optional) – A dictionary whose items are stored as attributes.
metadata (dict, optional) – A dictionary containing a set of parameters that will to stores in the metadata attribute. Some parameters might be mandatory in some cases.
original_metadata (dict, optional) – A dictionary containing a set of parameters that will to stores in the original_metadata attribute. It typically contains all the parameters that has been imported from the original data file.

angle(deg=False)

Return the angle (also known as phase or argument). If the data is real, the angle is 0 for positive values and 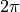$2\pi$ for negative values.

Parameters: deg (bool, optional) – Return angle in degrees if True, radians if False (default).
Returns: angle – The counterclockwise angle from the positive real axis on the complex plane, with dtype as numpy.float64.
Return type: HyperSpy signal

argand_diagram(*args, **kwargs)

Calculate and plot Argand diagram of complex signal

Parameters

size ([int, int], optional) – Size of the Argand plot in pixels (Default: [256, 256])
range (array_like, shape(2,2) or shape(2,) optional) – The position of the edges of the diagram (if not specified explicitly in the bins parameters): [[xmin, xmax], [ymin, ymax]]. All values outside of this range will be considered outliers and not tallied in the histogram. (Default: None)

Returns

Argand diagram as Signal2D

Return type

argand_diagram

Examples

>>> import hyperspy.api as hs
>>> holo = hs.datasets.example_signals.object_hologram()
>>> ref = hs.datasets.example_signals.reference_hologram()
>>> w = holo.reconstruct_phase(ref)
>>> w.argand_diagram(range=[-3, 3]).plot()